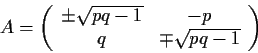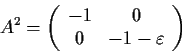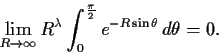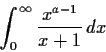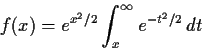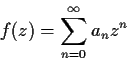Previous: Spring85
Next: Fall85
Preliminary Exam - Summer 1985
Problem 2
- For
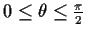 , show that
, show that
- By using Part 1, or by any other method, show that if
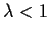 , then
, then
Problem 3
Let
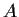
be a nonsingular real
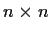
matrix. Prove that there
exists a unique orthogonal matrix
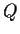
and a unique positive definite
symmetric matrix
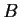
such that
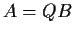
.
Problem 4
Let
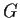
be a group of order
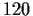
, let
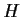
be a subgroup of order
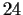
, and
assume that there is at least one left coset of
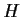
(other than
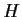
itself)
which is equal to some right coset of
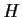
. Prove that
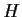
is a normal
subgroup of
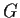
.
Problem 5
By the Fundamental Theorem of Algebra, the polynomial
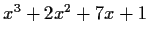
has
three complex roots,
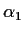
,
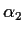
, and
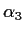
. Compute
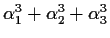
.
_Fundamental Theorem>of Algebra
Problem 6
Evaluate the integral
where
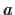
is a complex number. What restrictions must be put on
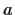
?
Problem 7
Let
for
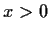
.
- Show that
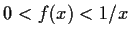 .
.
- Show that
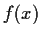 is strictly decreasing for
is strictly decreasing for 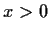 .
.
Problem 8
Let f be a real valued continuous function on a compact interval
![$[a,b]$](img43-25.gif)
. Given
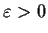
, show that there is a polynomial p
such that
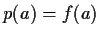
,
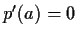
, and
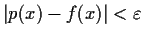
for
![$x\in [a,b]$](img48-25.gif)
.
Problem 10
Prove that for each
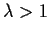
the equation
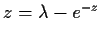
in
the half-plane
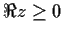
has exactly one root, and that this root is real.
Problem 11
- Let
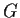 be a cyclic group, and let
be a cyclic group, and let 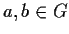 be elements which
are not squares. Prove that
be elements which
are not squares. Prove that 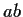 is a square.
is a square.
- Give an example to show that this result is false if the group
is not cyclic.
Problem 12
Let
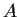
be an
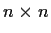
real matrix and
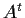
its
transpose. Show that
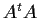
and
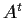
have the same
range.
Problem 13
Let
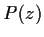
be a polynomial of degree
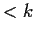
with complex coefficients.
Let
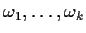
be the
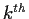
roots of unity in
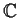
.
Prove that
Problem 14
Let
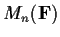
denote the ring of
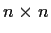
matrices over a field
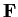
. For
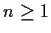
, does there exist a ring homomorphism from
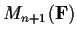
onto
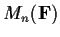
?
Problem 15
For each
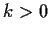
, let
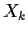
be the set of analytic functions
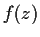
on the open unit disc
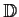
such that
is finite. Show that
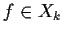
if and only if
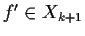
.
Problem 16
A function
![% latex2html id marker 1023
$f:[0,1]\to\mbox{$\mathbb{R}^{}$}$](img90-23.gif)
is said to be upper semicontinuous
if given
![$x \in [0,1]$](img91-23.gif)
and
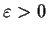
, there exists a
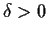
such that if
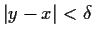
, then
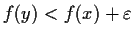
. Prove that
an upper semicontinuous function f on
![$[0,1]$](img96-23.gif)
is bounded above
and attains its maximum value at some point
![$p \in [0,1]$](img97-23.gif)
.
_function,>semicontinuous
Problem 17
Let
where all the
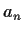
are nonnegative reals, and the series
has radius of convergence
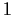
. Prove that
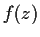
cannot be analytically
continued to a function analytic in a neighborhood of
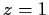
.
Problem 18
Solve the differential equations
Problem 19
Let
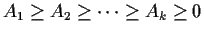
. Evaluate
Note: See also Problem
![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif)
.
Problem 20
Let
F be a field of characteristic
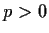
,
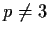
. If
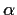
is a zero of the polynomial
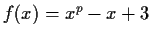
in an extension field
of
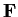
, show that
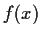
has
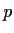
distinct zeros in the field
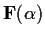
.



Previous: Spring85
Next: Fall85
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
 2 matrix
2 matrix 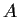 satisfies
satisfies 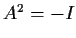 if and only if
if and only if
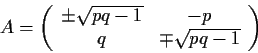
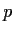 and
and 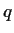 are real numbers such that
are real numbers such that 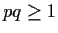 and both
upper or both lower signs should be chosen in the double signs.
and both
upper or both lower signs should be chosen in the double signs.
 2 matrix
2 matrix 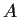 such that
such that
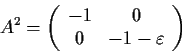
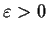 .
.