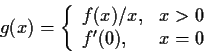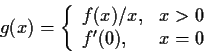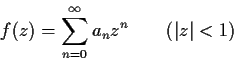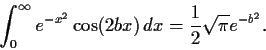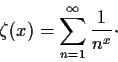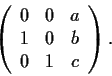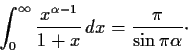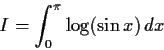Previous: Fall84
Next: Summer85
Preliminary Exam - Spring 1985
Problem 1
Let
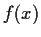
,
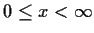
, be continuous, differentiable,
with
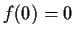
, and that
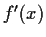
is an increasing function
of
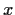
for
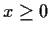
. Prove that
is an increasing function of
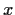
.
Problem 2
In a commutative group
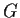
, let the element
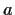
have order
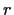
, let
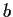
have order
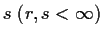
, and assume that the greatest
common divisor of
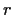
and
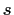
is
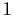
. Show that
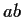
has order
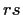
.
Problem 3
Show that a necessary and sufficient condition for three points
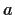
,
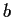
, and
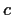
in the complex plane to form an equilateral triangle
is that
Problem 4
Let
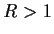
and let
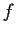
be analytic on
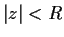
except at
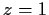
,
where
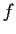
has a simple pole. If
is the Maclaurin series for
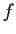
, show that
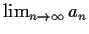
exists.
Problem 5
Factor
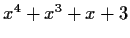
completely in
![% latex2html id marker 745
$\mbox{$\mathbb{Z}^{}$}_5[x]$](img32-24.gif)
.
Problem 6
Let
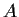
and
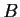
be two
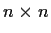
self-adjoint (i.e., Hermitian) matrices
over
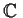
such that all eigenvalues of
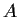
lie in
![$[a,a']$](img38-24.gif)
and all
eigenvalues of
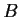
lie in
![$[b,b']$](img40-24.gif)
. Show that all eigenvalues of
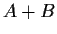
lie in
![$[a+b,a'+b']$](img42-24.gif)
.
Problem 7
Prove that
What restrictions, if any, need be placed on
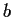
?
Problem 8
Let
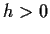
be given. Consider the linear difference equation
(Note the analogy with the differential equation
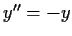
.)
- Find the general solution of
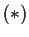 by trying suitable
exponential substitutions.
by trying suitable
exponential substitutions.
- Find the solution with
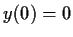 and
and 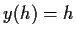 . Denote it by
. Denote it by
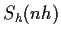 ,
,
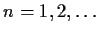 .
.
- Let
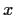 be fixed and
be fixed and 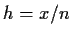 . Show that
. Show that
Problem 9
Define the function
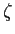
by
Prove that
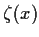
is defined and has continuous derivatives
of all orders in the interval
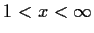
.
Problem 10
For arbitrary elements
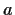
,
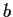
, and
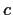
in a field
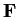
, compute the
minimal polynomial of the matrix
Problem 11
Let
![% latex2html id marker 910
$\mbox{\bf {F}} = \{a+b\sqrt[3]{2}+c\sqrt[3]{4} \;\vert\; a, b, c \in \mbox{$\mathbb{Q}\,^{}$}\}$](img65-24.gif)
.
Prove that
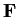
is a field and each element in
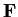
has a unique
representation
as
![$a+b\sqrt[3]{2}+c\sqrt[3]{4}$](img68-24.gif)
with
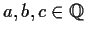
. Find
![$\left( 1-\sqrt[3]{2} \, \right)^{-1}$](img70-24.gif)
in
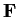
.
Problem 12
Prove that
What restrictions must be placed on
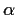
?
Problem 13
Prove that for any
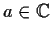
and any integer
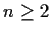
, the
equation
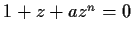
has at least one root in the disc
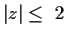
.
Problem 14
Show that
converges as an improper Riemann integral. Evaluate
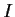
.
Problem 15
Let
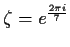
be a primitive
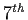
root of
unity. Find a cubic polynomial with integer coefficients having
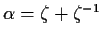
as a root.
Problem 16
Let f be continuous on
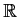
, and let
Prove that
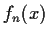
converges uniformly to a limit on every finite
interval
![$[a,b]$](img86-23.gif)
.
Problem 17
Let
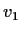
and
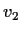
be two real valued continuous functions on
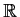
such that
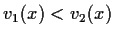
for all
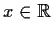
. Let
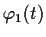
and
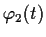
be, respectively, solutions of the differential equations
for
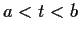
. If
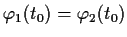
for some
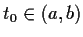
,
show that
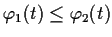
for all
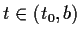
.
Problem 18
Let
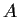
and
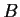
be two
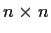
self-adjoint (i.e., Hermitian) matrices
over
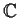
and assume
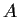
is positive definite. Prove that all eigenvalues
of AB are real.
Problem 19
Let
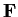
be a finite field. Give a complete proof of the fact that
the number of elements of
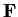
is of the form
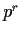
, where
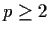
is
a prime number and
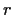
is an integer
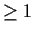
.
Problem 20
Let
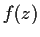
be an analytic function that maps the open disc
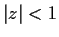
into itself. Show that
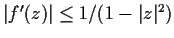
.



Previous: Fall84
Next: Summer85
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10