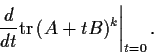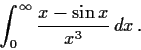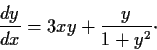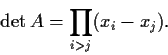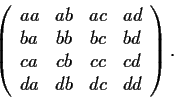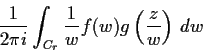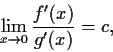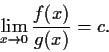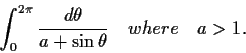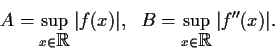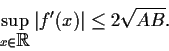Previous: Summer84
Next: Spring85
Preliminary Exam - Fall 1984
Problem 2
Let
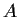
and
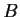
be n
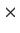
n real matrices, and k a positive
integer. Find
-
-
Problem 3
Prove or supply a counterexample: If
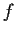
is a nondecreasing
real valued function on
![$[0,1]$](img16-23.gif)
, then there is a sequence
of continuous functions on
![$[0,1]$](img17-23.gif)
,
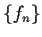
,
such
that for each
![$x \in [0,1]$](img19-23.gif)
,
Problem 5
Consider the differential equation
Prove
- For each
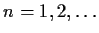 , there is a unique solution
, there is a unique solution
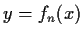 defined for
defined for
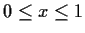 such that
such that 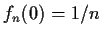 .
.
-
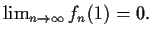
Problem 6
Let
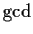
abbreviate greatest common divisor and
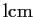
abbreviate
least common multiple. For three nonzero integers a, b, c, show
that
Problem 7
Let
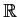
![$[x_1,\ldots,x_n]$](img32-23.gif)
be the polynomial ring
over the real field
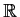
in the
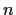
variables
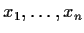
.
Let the matrix
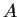
be the
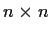
matrix whose
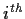
row is
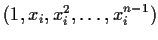
,
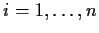
.
Show that
Problem 8
Let
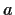
,
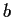
,
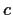
, and
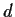
be real numbers, not all zero. Find the
eigenvalues of the following 4
4 matrix and describe
the eigenspace decomposition of
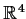
:
Problem 9
Let
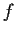
and
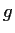
be analytic functions in the open unit disc,
and let
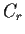
denote the circle with center
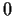
and radius
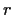
,
oriented counterclockwise.
- Prove that the integral
is independent of 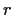 as long as
as long as 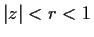 and that it
defines an analytic function
and that it
defines an analytic function 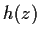 ,
, 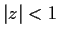 .
.
- Prove or supply a counterexample: If
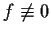 and
and
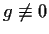 , then
, then
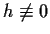 .
.
Problem 10
Prove or supply a counterexample:
- If
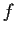 and
and 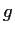 are
are 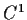 real valued functions on
real valued functions on 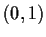 , if
, if
if 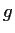 and
and 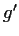 never vanish, and if
never vanish, and if
then
- Do the same question for complex valued
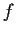 and
and 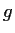 .
.
Problem 11
Show that all groups of order
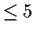
are commutative. Give an
example of a noncommutative group of order
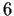
.
Problem 12
Let
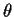
and
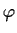
be fixed,
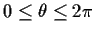
,
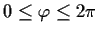
and let
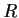
be the linear transformation
from
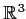
to
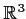
whose matrix in the standard basis
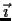
,
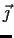
, and
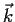
is
Let
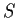
be the linear transformation of
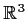
to
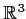
whose
matrix with respect to the basis
is
Prove that
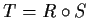
leaves a line invariant.
Problem 13
Show that if
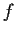
is a homeomorphism of
![$[0,1]$](img93-21.gif)
onto itself, then
there is a sequence
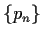
,
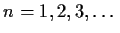
of polynomials
such that
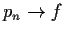
uniformly on
![$[0,1]$](img97-21.gif)
and each
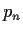
is a
homeomorphism of
![$[0,1]$](img99-21.gif)
onto itself.
Problem 15
Consider the differential equation
- Show that
decreases along solutions.
- Show that for any
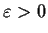 , there is a
, there is a 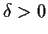 such
that whenever
such
that whenever
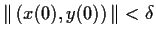 , there is a
unique solution
, there is a
unique solution
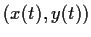 of the given equations with the initial
condition
of the given equations with the initial
condition
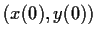 which is defined for all
which is defined for all 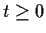 and
satisfies
and
satisfies
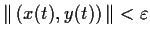 .
.
Problem 16
Let
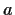
be an element in a field
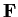
and let
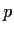
be a prime. Assume a
is not a
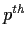
power. Show that the polynomial
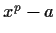
is
irreducible in
![% latex2html id marker 1124
$\mbox{\bf {F}}[x]$](img116-11.gif)
.
Problem 17
Let
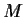
be the
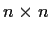
matrix over a field
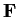
all of whose
entries are equal to
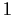
. Find the Jordan Canonical Form of
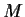
and
discuss the extent to which the Jordan form depends on the
characteristic of the field
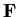
.
Problem 18
Let
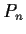
be the vector space of all real polynomials with degrees
at most n. Let
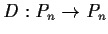
be given by differentiation:
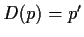
. Let
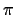
be a real polynomial. What is the
minimal polynomial of the transformation
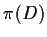
?
Problem 19
Prove or supply a counterexample: If
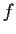
is a continuous complex
valued function defined on a connected open subset of the
complex plane and if
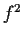
is analytic, then
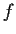
is analytic.
Problem 20
Let
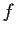
be a
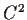
function on the real line. Assume
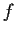
is
bounded with bounded second derivative. Let
Prove that



Previous: Summer84
Next: Spring85
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
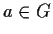 , then
, then 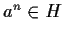 .
.
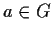 , then for some
, then for some 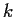 ,
, 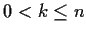 , we have
, we have 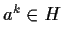 .
.