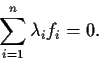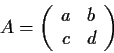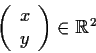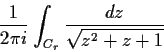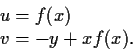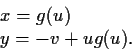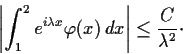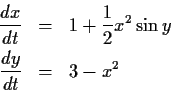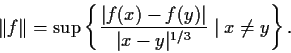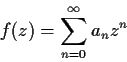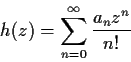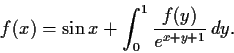Previous: Spring84
Next: Fall84
Preliminary Exam - Summer 1984
Problem 1
Show that if a subgroup
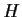
of a group
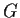
has just one left coset different
from itself, then it is a normal subgroup of
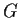
.
Problem 2
Let
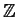
be the ring of integers and
![% latex2html id marker 687
$\mbox{$\mathbb{Z}^{}$}[x]$](img5-22.gif)
the polynomial ring over
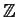
.
Show that
is irreducible in
![% latex2html id marker 693
$\mbox{$\mathbb{Z}^{}$}[x]$](img8-22.gif)
.
Problem 3
Let
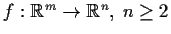
, be a linear transformation of
rank
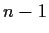
. Let
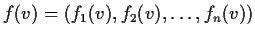
for
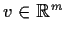
. Show that a necessary and sufficient condition for
the system of inequalities
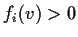
,
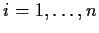
, to have no
solution is that there exist real numbers
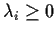
, not all
zero, such that
Problem 4
Let
be a real matrix with
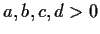
. Show that
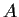
has an eigenvector
with
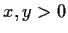
.
Problem 6
Let
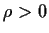
. Show that for
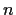
large enough, all the zeros of
lie in the circle
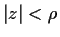
.
Problem 7
Let
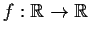
be
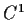
and let
If
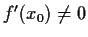
, show that this transformation is locally invertible
near
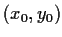
and the inverse has the form
Problem 8
Let
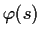
be a
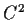
function on
![$[1,2]$](img41-22.gif)
with
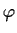
and
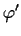
vanishing at
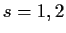
. Prove that there is a constant
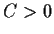
such
that for any
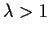
,
Problem 9
Consider the solution curve
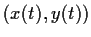
to the equations
with initial conditions
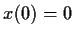
and
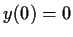
. Prove that the solution
must cross the line
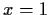
in the
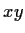
plane by the time
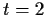
.
Problem 10
Let
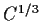
be the set of real valued functions f on the closed
interval
![$[0,1]$](img56-22.gif)
such that
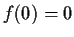 ;
;
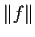 is finite, where by definition
is finite, where by definition
Verify that
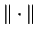
is a norm for the space
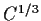
, and prove that
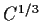
is complete with respect to this norm.
Problem 11
Let
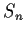
denote the group of permutations of
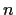
letters. Find
four different subgroups of
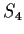
isomorphic to
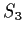
and nine
isomorphic to
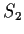
.
Problem 13
Let
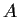
be a 2
2 matrix over
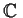
which is not a scalar
multiple of the identity matrix
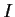
. Show that any 2
2
matrix
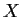
over
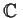
commuting with
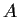
has the form
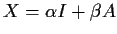
,
where
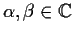
.
Problem 14
Suppose
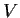
is an
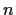
-dimensional vector space over the field
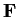
. Let
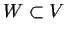
be a subspace of dimension
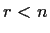
. Show that
Problem 15
Let
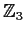
be the field of integers
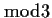
and
![% latex2html id marker 1132
$\mbox{$\mathbb{Z}^{}$}_3[x]$](img101-19.gif)
the
corresponding polynomial ring. Decompose
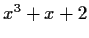
into irreducible
factors in
![% latex2html id marker 1138
$\mbox{$\mathbb{Z}^{}$}_3[x]$](img103-16.gif)
.
Problem 16
Let
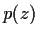
be a nonconstant polynomial with real coefficients such
that for some real number
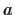
,
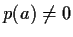
but
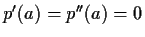
. Prove that the equation
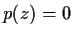
has a nonreal root.
Problem 17
Suppose
has radius of convergence
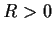
. Show that
is entire and that for
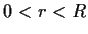
, there is a constant
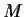
such that
Problem 18
Show that there is a unique continuous function
![% latex2html id marker 1198
$f:[0,1]\to\mbox{$\mathbb{R}^{}$}$](img115-11.gif)
such that
Problem 19
Let
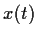
be the solution of the differential equation
with initial conditions
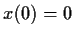
and
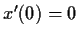
. Show that for
suitable constants
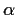
and
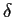
,



Previous: Spring84
Next: Fall84
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10