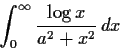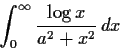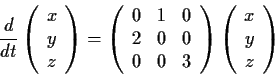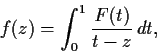Previous: Fall83
Next: Summer84
Preliminary Exam - Spring 1984
Problem 1
Evaluate
for

.
Problem 2
For a
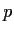
-group of order
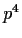
, assume the center of
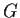
has order
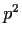
.
Determine the number of conjugacy classes of
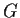
.
Problem 3
Let
![% latex2html id marker 686
$f : [0,1] \to \mbox{$\mathbb{R}^{}$}$](img8-20.gif)
be continuous, with
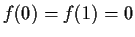
. Assume
that
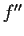
exists on
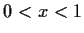
, with

. Show that
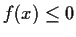
for all
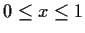
.
Problem 4
Which number is larger,
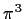
or
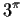
?
Problem 5
Let
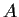
and
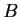
be complex
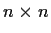
matrices such that

, and assume
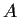
has no eigenvalues of absolute
value
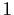
. Prove that
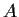
and
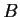
have a common (nonzero) eigenvector.
Problem 6
Let
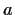
be a positive real number. Define a sequence
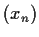
by
Find a necessary and sufficient condition on
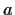
in order that a
finite limit
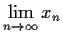
should exist.
Problem 7
Find the number of roots of
which lie between the two circles
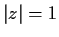
and
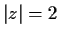
.
Problem 8
Show that the system of differential equations
has a solution which tends to
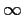
as
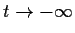
and tends to
the origin as

.
Problem 9
Let
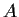
be a real
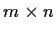
matrix with rational entries and let b be
an
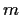
-tuple of rational numbers. Assume that the system of
equations
Ax = b has a solution x in complex
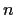
-space
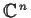
. Show that
the equation
has a solution vector with rational components, or give a counterexample.
Problem 10
Let

be a principal ideal domain and let

and
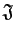
be nonzero ideals in
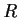
. Show that
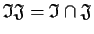
if and only if
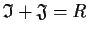
.
Problem 11
Prove the following statement or supply a counterexample: If
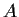
and

are real
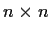
matrices which are similar over
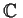
,
then
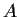
and
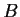
are similar over
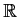
.
Problem 12
Consider the equation
Show that there is an
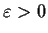
such that if
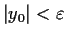
,
then the solution
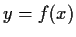
with
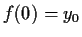
satisfies
Problem 13
Let
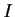
be an open interval in
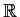
containing zero. Assume that

exists on a neighborhood of zero and

exists. Show
that
(
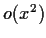
denotes a quantity such that
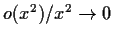
as
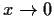
).
Problem 14
Let
be a field and let

be a finite set. Let
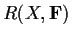
be the
ring of all functions from
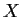
to
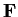
, endowed with the pointwise
operations. What are the maximal ideals of
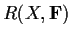
?
Problem 15
Let
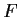
be a continuous complex valued function on the interval
![$[0,1]$](img76-19.gif)
. Let
for

a complex number not in
![$[0,1]$](img79-19.gif)
.
- Prove that
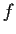 is an analytic function.
is an analytic function.
- Express the coefficients of the Laurent series of
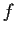 about
about  in terms of
in terms of 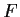 . Use your result to show that
. Use your result to show that
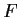 is uniquely determined by
is uniquely determined by 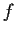 .
.
Problem 16
Prove, or supply a counterexample: If
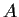
is an invertible

complex matrix and some power of
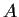
is diagonal,
then

can be diagonalized.
Problem 17
Prove that the Taylor coefficients at the origin of the function
are rational numbers.
Problem 18
Prove or supply a counterexample: If the function
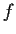
from
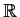
to
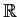
has both a left limit and a right limit at each point of
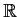
, then the set of discontinuities of
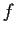
is, at most, countable.
Problem 19
Let
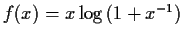
,
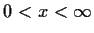
.
- Show that
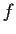 is strictly monotonically increasing.
is strictly monotonically increasing.
- Compute
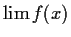 as
as 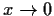 and
and  .
.
Problem 20
Determine all finitely generated abelian groups
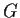
which have only
finitely many automorphisms.



Previous: Fall83
Next: Summer84
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10