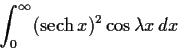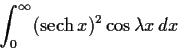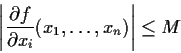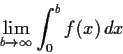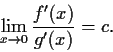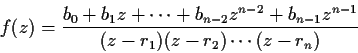Previous: Summer83
Next: Spring84
Preliminary Exam - Fall 1983
Problem 1
Evaluate
where
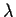
is a real constant and
Problem 2
Let
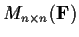
denote the ring of n
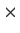
n
matrices over a field
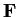
. For
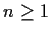
does there exist a ring homomorphism from
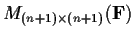
onto
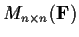
?
Problem 3
Let
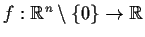
be a function which is continuously
differentiable and whose partial derivatives are uniformly bounded:
for all
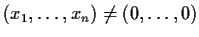
. Show that if
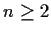
, then
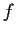
can be extended to a continuous function defined on all of
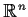
. Show
that this is false if
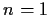
by giving a counterexample.
Problem 4
Prove or disprove (by giving a counterexample), the following
assertion: Every infinite sequence
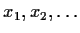
of real numbers
has either a nondecreasing subsequence or a nonincreasing subsequence.
Problem 5
Let
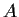
be the
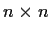
matrix which has zeros on the main diagonal
and ones everywhere else. Find the eigenvalues and eigenspaces of
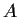
and
compute
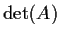
.
Problem 6
Consider the polynomial
How many zeros (counting multiplicities) does
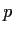
have in the annular
region
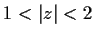
?
Problem 7
Let
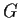
be a finite group and
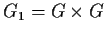
. Suppose that
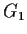
has exactly four normal subgroups. Show that
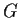
is simple and nonabelian.
Problem 8
Let
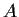
be a linear transformation on
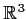
whose matrix (relative to
the usual basis for
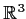
) is both symmetric and orthogonal. Prove
that
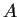
is either plus or minus the identity, or a rotation by
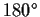
about some axis in
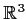
, or a reflection about some
two-dimensional subspace of
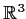
.
Problem 9
For which real values of
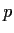
does the differential equation
admit solutions
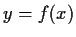
with infinitely many critical points?
Problem 10
Let
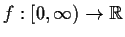
be a uniformly continuous function with
the property that
exists (as a finite limit). Show that
Problem 11
Prove or supply a counterexample:
If
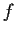
and
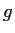
are
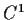
real valued functions on
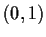
, if
if
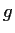
and
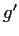
never vanish, and if
then
Problem 12
Let
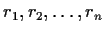
be distinct complex numbers. Show that a
rational function of the form
can be written as a sum
for suitable constants
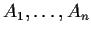
.
Problem 14
Let
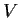
be a finite-dimensional complex vector space and let
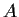
and
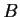
be
linear operators on
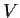
such that
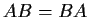
. Prove that if
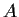
and
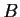
can
each be diagonalized, then there is a basis for
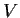
which simultaneously
diagonalizes
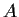
and
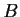
.
Problem 16
Let
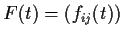
be an n

n matrix of continuously
differentiable functions
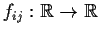
, and let
Show that u is differentiable and
Problem 17
Prove that every finite integral domain is a field.
Problem 18
Let
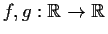
be smooth functions with
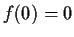
and
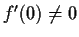
. Consider the equation
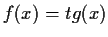
,
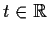
.
- Show that in a suitably small interval
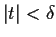 , there is
a unique continuous function
, there is
a unique continuous function 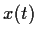 which solves the equation and
satisfies
which solves the equation and
satisfies 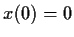 .
.
- Derive the first order Taylor expansion of
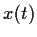 about
about 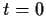 .
.
Problem 19
Prove that if
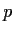
is a prime number, then the polynomial
is irreducible in
![% latex2html id marker 1148
$\mathbb{Q}[x]$](img103-15.gif)
.
Problem 20
Let m and n be positive integers, with
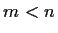
. Let
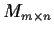
be the
space of linear transformations of
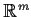
into
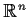
(considered as
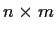
matrices) and let
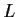
be the set of transformations in
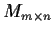
which have rank m.
- Show that
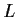 is an open subset of
is an open subset of 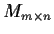 .
.
- Show that there is a continuous function
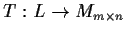 such
that
such
that
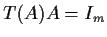 for all
for all 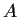 , where
, where 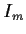 is the identity on
is the identity on
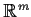 .
.



Previous: Summer83
Next: Spring84
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10