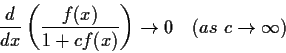Previous: Spring83
Next: Fall83
Preliminary Exam - Summer 1983
Problem 1
The number
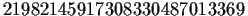
is the thirteenth power
of a positive integer. Which positive integer?
Problem 2
Let
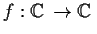
be an analytic function such that
is bounded for some k and m. Prove that
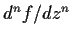
is
identically zero for sufficiently large n. How large must n be,
in terms of k and m?
Problem 3
Let
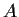
be an
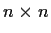
complex matrix, and let
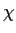
and
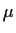
be the characteristic and minimal polynomials of
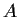
.
Suppose that
Determine the Jordan Canonical Form of
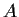
.
Problem 4
Outline a proof, starting from basic properties of the real numbers, of the
following theorem: Let
![% latex2html id marker 716
$f:[a,b] \to \mbox{$\mathbb{R}^{}$}$](img13-19.gif)
be a continuous function
such that
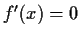
for all
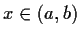
. Then

.
Problem 5
Let
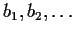
be positive real numbers with
Assume also that
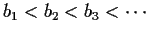
. Show that
the set of quotients
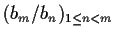
is dense in

.
Problem 6
Let
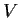
be a real vector space of dimension
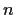
with a positive definite
inner product. We say that two bases
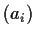
and
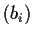
have the
same orientation if the matrix of the change of basis from
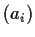
to
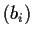
has a positive determinant. Suppose now that
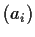
and
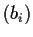
are orthonormal bases with the same orientation. Show that
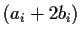
is again a basis of
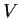
with the same orientation as

.
Problem 7
Compute
where

is a constant.
Problem 8
Let
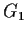
,
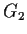
, and
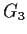
be finite groups, each of which is generated
by its commutators (elements of the form
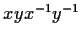
). Let

be
a subgroup of
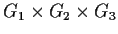
, which maps surjectively,
by the natural projection map, to
the partial products
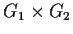
,
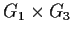
and
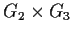
.
Show that
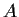
is equal to
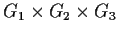
.
Problem 9
Suppose
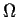
is a bounded domain in

with a boundary consisting
of a smooth Jordan curve
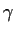
. Let
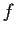
be holomorphic in a
neighborhood of the closure of
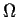
, and suppose that
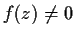
for
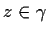
. Let
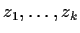
be the zeros of
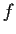
in
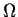
, and let

be the order of the zero of
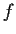
at
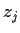
(for
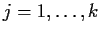
).
- Use Cauchy's integral formula to show that
- Suppose that
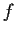 has only one zero
has only one zero 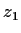 in
in 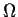 with
multiplicity
with
multiplicity 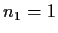 . Find a boundary integral involving
. Find a boundary integral involving 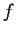 whose
value is the point
whose
value is the point 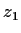 .
.
Problem 10
Let
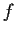
be a twice differentiable real valued function on
![$[0,2\pi]$](img68-19.gif)
, with

. Show that
Problem 11
Find the eigenvalues, eigenvectors, and the Jordan Canonical Form of
considered as a matrix with entries in
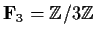
.
Problem 12
Prove that a continuous function from
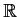
to
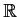
which maps
open sets to open sets must be monotonic.
Problem 13
Let
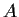
be an n
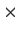
n complex matrix, all of whose eigenvalues are
equal to
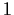
. Suppose that the set
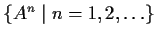
is
bounded. Show that

is the identity matrix.
Problem 14
Let
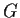
be a transitive subgroup of the group
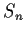
of permutations of
the set
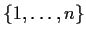
. Suppose that
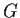
is a simple group and that
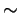
is an equivalence relation on
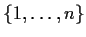
such that
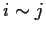
implies that
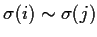
for all
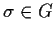
. What can
you conclude about the relation

?
Problem 15
Let
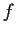
be analytic on and inside the unit circle
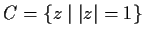
.
Let
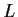
be the length of the image of

under

. Show that
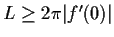
.
Problem 16
Let

be an open subset of
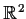
, and let

be a smooth map. Assume that
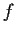
preserves orientation and maps any pair
of orthogonal curves to a pair of orthogonal curves. Show that
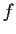
is
holomorphic.
Note: Here we identify
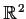 with
with
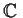 .
.
Problem 17
Let
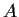
be an
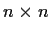
Hermitian matrix satisfying the condition
Show that
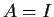
.
Problem 18
Find all real valued
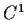
solutions
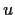
of the differential equation
Problem 19
Compute the area of the image of the unit disc
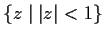
under the map
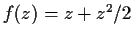
.
Problem 20
Let
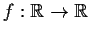
be continuously differentiable, periodic of
period

, and nonnegative. Show that
uniformly in
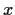
.



Previous: Spring83
Next: Fall83
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10




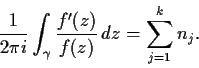
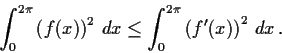
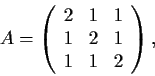
![]() with
with
![]() .
.