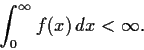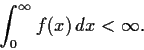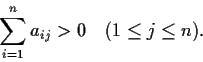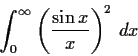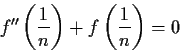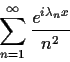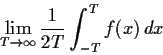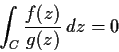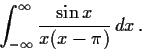Previous: Fall82
Next: Summer83
Preliminary Exam - Spring 1983
Problem 1
Let
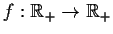
be a monotone decreasing function, defined
on the positive real numbers with
Show that
Problem 2
Let
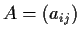
be an n

n real matrix satisfying the
conditions:
Show that
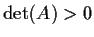
.
Problem 3
A fractional linear transformation maps the annulus
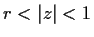
(where
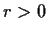
) onto the domain bounded by the two circles
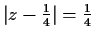
and
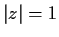
. Find
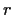
.
Problem 4
In the triangular network in
depicted below, the
points
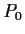
,
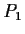
,
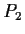
, and
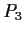
are respectively
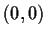
,
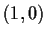
,
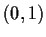
, and
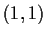
. Describe the structure of the group of all
Euclidean transformations of
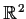
which leave this network invariant.
file=../Fig/Pr/Sp83-4,width=2.7in
Problem 5
Find all solutions
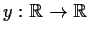
to
Problem 6
Suppose that
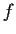
is a continuous function on
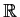
which is periodic
with period
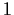
, i.e.,
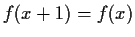
. Show:
- The function
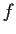 is bounded above and below and achieves
its maximum and minimum.
is bounded above and below and achieves
its maximum and minimum.
- The function
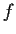 is uniformly continuous on
is uniformly continuous on 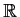 .
.
- There exists a real number
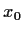 such that
such that
Problem 7
Let
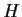
be the group of integers

, under addition, where
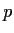
is a prime
number. Suppose that
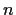
is an integer satisfying
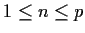
,
and let
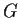
be the group
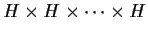
(
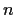
factors).
Show that
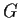
has no automorphism of order
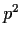
.
Problem 8
Suppose that
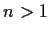
is an integer. Prove that the sum
is not an integer.
Problem 9
Suppose that
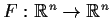
is continuous and satisfies
for all
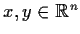
and some
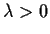
.
Prove that
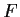
is one-to-one, onto, and has a continuous inverse.
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 10
Evaluate
and justify your calculations.
Problem 11
Let
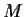
be an invertible real
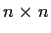
matrix. Show that there is
a decomposition
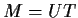
in which
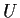
is an
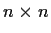
real orthogonal
matrix and
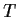
is upper-triangular with positive diagonal entries.
Is this decomposition unique?
Problem 12
Determine all the complex analytic functions
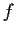
defined on the unit
disc
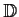
which satisfy
for
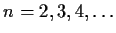
.
Problem 13
Let
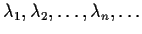
be real numbers. Show
that the infinite series
converges uniformly over
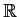
to a continuous limit function
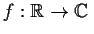
. Show, further, that the limit
exists.
Problem 14
Let
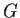
be an abelian group which is generated by, at most,
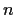
elements.
Show that each subgroup of
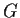
is again generated by, at most,
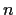
elements.
Problem 15
Let
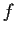
and
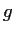
be complex polynomials with the degree of
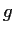
at least
two more than the degree of
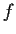
. Show that there is a positive number
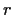
such that
for each simple closed curve
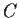
which does not intersect
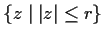
.
Problem 16
Let
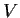
be a real vector space of dimension
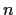
, and let
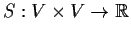
be a nondegenerate bilinear form. Suppose that
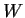
is a linear subspace of
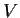
such that the restriction of
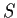
to
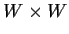
is identically
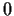
. Show that
we have
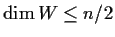
.
Problem 18
Let
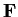
be the field with seven elements. How many 3
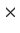
3 matrices
with coefficients in
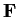
have determinant
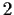
? How many have determinant
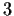
?
Problem 19
Show that the initial value problem
has a solution defined on all of
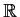
.
Problem 20
Show that the interval
![$[0,1]$](img98-14.gif)
cannot be written as a countably
infinite disjoint union of closed subintervals of
![$[0,1]$](img99-14.gif)
.



Previous: Fall82
Next: Summer83
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10