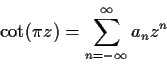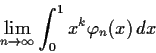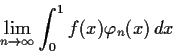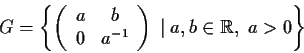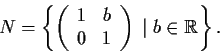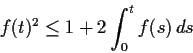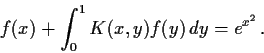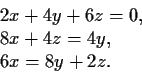Previous: Summer82
Next: Spring83
Preliminary Exam - Fall 1982
Problem 2
Consider the polynomial ring
![% latex2html id marker 723
$R = \mbox{$\mathbb{Z}^{}$}[x]$](img12-18.gif)
and the ideal
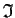
of
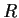
generated by
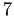
and
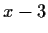
.
- Show that for each
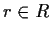 , there is an integer
, there is an integer 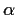 satisfying
satisfying
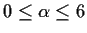 such that
such that
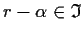 .
.
- Find
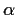 in the special case
in the special case
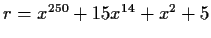 .
.
Problem 3
Let
be the Laurent expansion for
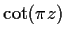
on the annulus
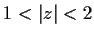
. Compute the
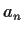
for
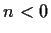
.
Problem 4
Let
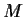
be an
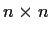
matrix of real numbers. Prove or disprove: The
dimension of the subspace of
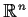
generated by the rows of
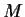
is equal to
the dimension of the subspace of
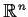
generated by the columns of
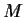
.
Problem 5
Let
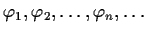
be nonnegative continuous
functions on
![$[0,1]$](img35-18.gif)
such that the limit
exists for every
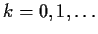
. Show that the limit
exists for every continuous function f on
![$[0,1]$](img39-18.gif)
.
Problem 6
Let
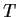
be a linear transformation on a finite-dimensional
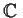
-vector space V,
and let
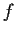
be a polynomial with coefficients in
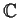
. If
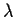
is an
eigenvalue of
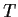
, show that
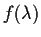
is an eigenvalue of
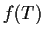
. Is
every eigenvalue of
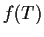
necessarily obtained in this way?
Problem 8
Let
- Show that
 is a normal subgroup of
is a normal subgroup of 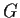 and prove that
and prove that 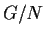 is
isomorphic to
is
isomorphic to 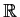 .
.
- Find a normal subgroup
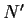 of
of 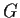 satisfying
satisfying
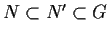 (where the inclusions are proper), or prove that there is no such subgroup.
(where the inclusions are proper), or prove that there is no such subgroup.
Problem 9
Let f be a real valued continuous nonnegative function on
![$[0,1]$](img59-18.gif)
such that
for
![$t \in [0,1]$](img61-18.gif)
. Show that
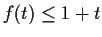
for
![$t \in [0,1]$](img63-18.gif)
.
Problem 10
Let
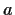
and
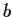
be complex numbers whose real parts are negative or
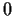
.
Prove the inequality
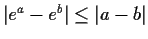
.
Problem 11
- Prove that there is no continuous map from the closed
interval
![$[0,1]$](img68-18.gif) onto the open interval
onto the open interval 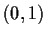 .
.
- Find a continuous surjective map from the open interval
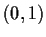 onto the closed interval
onto the closed interval ![$[0,1]$](img71-18.gif) .
.
- Prove that no map in Part 2 can be bijective.
Problem 12
Let
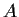
and
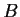
be complex
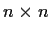
matrices having the same rank. Suppose
that
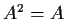
and
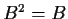
. Prove that
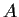
and
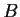
are similar.
Problem 13
Let
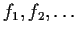
be continuous functions on
![$[0,1]$](img80-17.gif)
satisfying
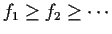
and such that
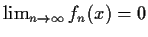
for each x. Must the
sequence
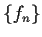
converge to
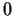
uniformly on
![$[0,1]$](img85-17.gif)
?
Problem 14
Let
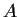
be an
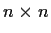
complex matrix, and let
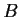
be the Hermitian
transpose of
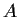
(i.e.,
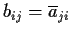
). Suppose that
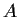
and
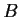
commute with each other. Consider the linear transformations
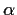
and
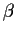
on
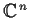
defined by
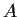
and
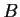
. Prove that
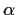
and
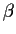
have the same image and the same kernel.
Problem 15
Let
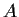
be a subgroup of an abelian group
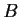
. Assume that
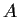
is a
direct summand of
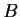
, i.e., there exists a subgroup
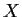
of
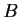
such that
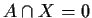
and such that
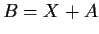
. Suppose that
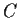
is a
subgroup of
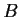
satisfying
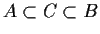
. Is
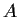
necessarily a direct summand of
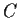
?
Problem 16
Find all pairs of
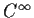
functions
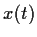
and
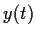
on
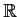
satisfying
Problem 18
Let
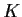
be a continuous function on the unit square
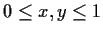
satisfying
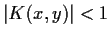
for all
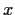
and
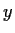
. Show that there is a
continuous function
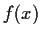
on
![$[0,1]$](img125-6.gif)
such that we have
Can there be more than one such function
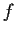
?
Problem 19
Let
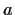
and
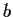
be nonzero complex numbers and
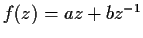
.
Determine the image under
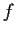
of the unit circle
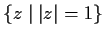
.
Problem 20
Let
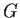
be the abelian group given by generators
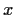
,
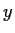
, and
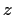
and by
the three relations:
Write
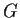
as a product of cyclic groups. How many elements of
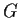
have
order
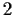
?



Previous: Summer82
Next: Spring83
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
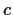 , show that
, show that 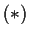 has a unique, continuously
differentiable solution
has a unique, continuously
differentiable solution 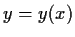 on a neighborhood of
on a neighborhood of 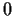 which satisfies
the initial condition
which satisfies
the initial condition 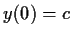 .
.
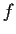 under which the solution
under which the solution 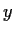 exists for
all
exists for
all
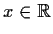 , for every initial value
, for every initial value  .
.