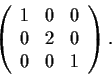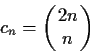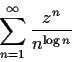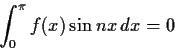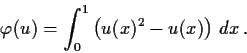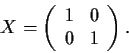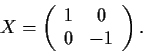Previous: Spring82
Next: Fall82
Preliminary Exam - Summer 1982
Problem 1
Determine the Jordan Canonical Form of the matrix
Problem 2
Compute the integral
Problem 3
Let 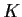 be a nonempty compact set in a metric space with distance
function
be a nonempty compact set in a metric space with distance
function 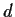 . Suppose that
. Suppose that
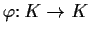 satisfies
satisfies
for all
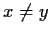
in
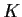
. Show there exists precisely one point
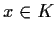
such
that
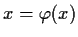
.
Problem 4
Let
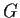
be a group with generators
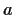
and
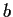
satisfying
Is
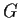
trivial?
Problem 5
Let
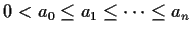
. Prove that the equation
has no roots in the disc
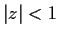
.
Problem 6
Suppose
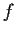
is a differentiable real valued function such that
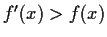
for all
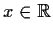
and
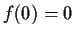
. Prove that
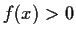
for all positive
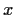
.
Problem 7
Let
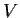
be the vector space of all real 3
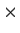
3 matrices and let
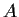
be
the diagonal matrix
Calculate the determinant of the linear transformation
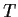
on
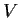
defined by
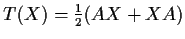
.
Problem 8
Let n be a positive integer.
- Show that the binomial coefficient
is even.
- Prove that
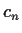 is divisible by
is divisible by 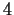 if and only if
n is not a power of
if and only if
n is not a power of 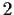 .
.
Problem 9
Determine the complex numbers
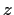
for which the power series
and its term by term derivatives of all orders converge absolutely.
Problem 10
For complex numbers
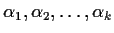
, prove
Note: See also Problem
![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif)
.
Problem 11
Let
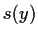
and
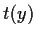
be real differentiable functions of
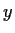
,
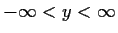
, such that the complex function
is complex analytic with
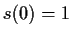
and
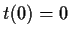
. Determine
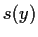
and
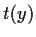
.
Problem 12
Determine (with proofs) which of the following polynomials are irreducible
over the field
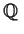
of rationals.
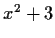
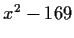
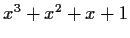
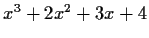 .
.
Problem 13
Let
![% latex2html id marker 896
$f:[0,\pi] \to \mbox{$\mathbb{R}^{}$}$](img54-15.gif)
be continuous and such that
for all integers
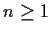
. Is
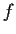
identically
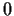
?
Problem 14
Let
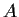
be a real
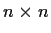
matrix such that
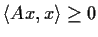
for
every real
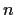
-vector
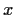
. Show that
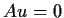
if and only if
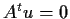
.
Problem 15
Let
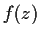
be analytic on the open unit disc
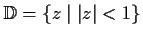
.
Prove that there is a sequence
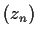
in
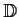
such that
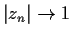
and
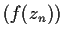
is bounded.
Problem 17
Let
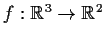
and assume that
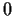
is a regular value of f
(i.e., the differential of
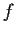
has rank
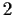
at each point of
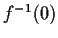
).
Prove that
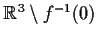
is arcwise connected.
Problem 18
Let
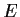
be the set of all continuous real valued functions
![% latex2html id marker 1026
\(u:[0,1]\to\mbox{$\mathbb{R}^{}$}\)](img87-14.gif)
satisfying
Let
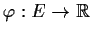
be defined by
Show that
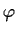
achieves its maximum value at some element
of
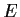
.
Problem 19
Let
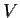
be a finite-dimensional vector space over the rationals
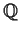
and
let
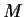
be an automorphism of
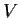
such that
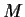
fixes no
nonzero vector in
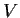
. Suppose that
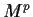
is the identity map on V,
where
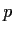
is a prime number. Show that the dimension of
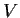
is
divisible by
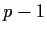
.
Problem 20
Let
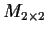
be the four-dimensional vector space of all 2
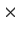
2 real matrices
and define
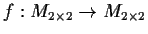
by
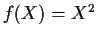
.
- Show that
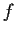 has a local inverse near the point
has a local inverse near the point
- Show that
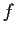 does not have a local inverse near the point
does not have a local inverse near the point



Previous: Spring82
Next: Fall82
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
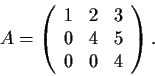



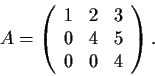
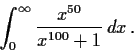
![]() be a nonempty compact set in a metric space with distance
function
be a nonempty compact set in a metric space with distance
function ![]() . Suppose that
. Suppose that
![]() satisfies
satisfies