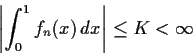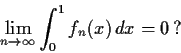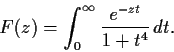Previous: Fall81
Next: Summer82
Preliminary Exam - Spring 1982
Problem 1
Prove the Fundamental Theorem of Algebra: Every nonconstant polynomial
with complex coefficients has a complex root.
_Fundamental Theorem>of Algebra
Problem 2
Let

be a subset which is uncountable. Prove that there
is a sequence of distinct points in
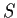
converging to a point of

.
Problem 3
Let
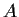
and
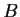
be n
n complex matrices. Prove that
Problem 4
Let
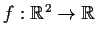
have directional derivatives in all
directions at the origin. Is
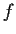
differentiable at the origin?
Prove or give a counterexample.
Problem 5
Let

be a sequence of twice differentiable functions on
![$[0,1]$](img11-14.gif)
such that
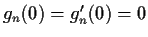
for all n. Suppose also that
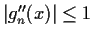
for all n and all
![$x \in [0,1]$](img14-14.gif)
. Prove that there
is a subsequence of

which converges uniformly on
![$[0,1]$](img16-14.gif)
.
Problem 6
Suppose that
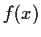
is a polynomial with real coefficients and
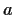
is a
real number with
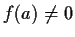
. Show that there exists a real polynomial
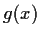
such that if we define
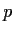
by
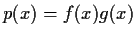
, we have
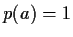
,
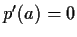
, and
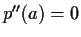
.
Problem 7
Suppose that the group
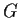
is generated by elements
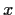
and
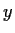
that satisfy
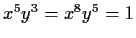
. Is

the trivial group?
Problem 8
Find
by contour integration.
Problem 9
Find the Jordan Canonical Form for the matrix (over
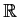
)
Problem 10
Prove that any group of order
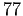
is cyclic.
Problem 11
Decide, without too much computation, whether a finite limit
exists, where z is a complex variable, and if yes, compute the limit.
Problem 12
Prove or give a counterexample: Every connected, locally pathwise
connected set in
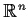
is pathwise connected.
Problem 13
Let
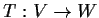
be a linear transformation between finite-dimensional
vector spaces. Prove that
Problem 14
Let
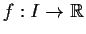
(where
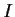
is an interval of
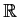
) be such
that
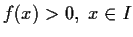
. Suppose that
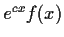
is
convex in

for every real number c. Show that
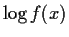
is
convex in

.
Note: A function
 is convex if
is convex if
for all
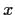
and
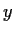
in
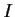
and

.
_function,>convex
Problem 15
How many nonsingular 2

2 matrices are there over the field of p
elements?
Problem 16
Prove that if

is a group containing no subgroup of index
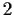
,
then any subgroup of index
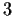
is normal.
Problem 17
Let
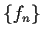
be a sequence of continuous functions from
![$[0,1]$](img58-14.gif)
to

. Suppose that
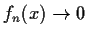
as

for
each
![$x \in [0,1]$](img62-14.gif)
and also that, for some constant
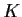
, we have
for all n. Does
Problem 18
For

, define
Show that F(z) is continuous for
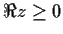
and analytic
for
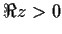
.
Problem 19
Show that the initial value problem
has a solution defined for
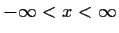
.
Problem 20
Prove that the polynomial
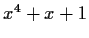
is irreducible over
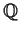
.



Previous: Fall81
Next: Summer82
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



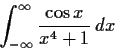
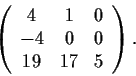
![]() is convex if
is convex if