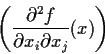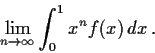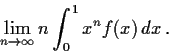Previous: Summer81
Next: Spring82
Preliminary Exam - Fall 1981
Problem 1
Evaluate the integral
Problem 2
Consider an autonomous system of differential equations
where
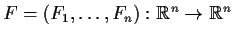
is a
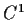
vector field.
- Let
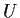 and
and 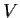 be two solutions on
be two solutions on 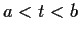 . Assuming that
. Assuming that
for all x, z in
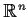 , show that
, show that
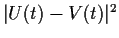 is a decreasing function of
is a decreasing function of 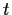 .
.
- Let
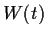 be a solution defined for
be a solution defined for 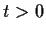 . Assuming that
. Assuming that
show that there exists
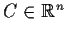 such that
such that
Problem 3
Let
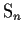
be the group of all permutations of
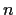
objects
and let
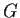
be a subgroup of
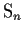
of order
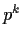
, where
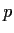
is
a prime not dividing
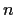
. Show that
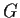
has a
fixed point; that is,
one of the objects is left fixed by every element of
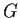
.
_group,>fixed point
Problem 5
The Fibonacci numbers
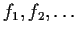
are defined recursively by
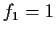
,
_Fibonacci numbers
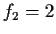
, and
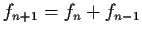
for
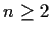
. Show that
exists, and evaluate the limit.
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 6
Let
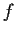
and
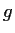
be continuous functions on
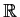
such that
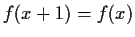
,
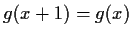
, for all
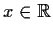
.
Prove that
Problem 7
Find a specific polynomial with rational coefficients having
![$\sqrt{2}+\sqrt[3]{3}$](img48-17.gif)
as a root.
Problem 8
- How many zeros does the function
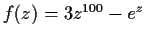 have inside
the unit circle (counting multiplicities)?
have inside
the unit circle (counting multiplicities)?
- Are the zeros distinct?
Problem 9
Let
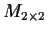
be the vector space of all real 2
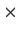
2 matrices. Let
and define a linear transformation
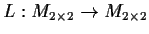
by
L(X) = AXB. Compute the trace and the determinant of
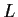
.
Problem 10
Let
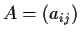
be an
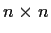
matrix whose entries
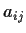
are
real valued differentiable functions defined on
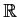
. Assume that the
determinant
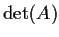
of
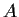
is everywhere positive. Let
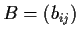
be the inverse matrix of
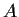
. Prove the formula
Problem 11
Consider the complex 3
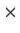
3 matrix
where
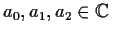
.
- Show that
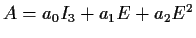 , where
, where
- Use Part 1 to find the complex eigenvalues of
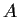 .
.
- Generalize Parts 1 and 2 to n
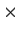 n matrices.
n matrices.
Problem 12
Let a, b be real constants and let
Show that u is harmonic and find an entire function f(z)
whose real part is u.
Correction: 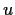 cannot be the real part of an entire function.
Why? Change
cannot be the real part of an entire function.
Why? Change 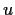 slightly and do the problem.
slightly and do the problem.
Problem 13
Let
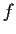
be a real valued function on
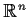
of class
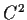
. A point
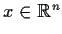
is a critical point of f if all the partial
derivatives of f vanish at x; a critical point is nondegenerate
if the
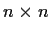
matrix
is nonsingular.
Let x be a nondegenerate critical point of f. Prove that there
is an open neighborhood of x which contains no other critical
points (i.e., the nondegenerate critical points are isolated).
Problem 14
Let
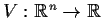
be a
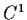
function and consider the system
of second order differential equations
where
Let
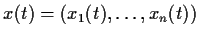
be a solution of this system
on a finite interval
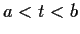
.
- Show that the function
is constant for 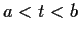 .
.
- Assuming that
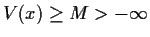 for all
for all
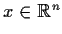 ,
show that
,
show that 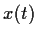 ,
, 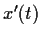 , and
, and 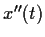 are bounded on
are bounded on 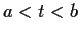 ,
and then prove all three limits
,
and then prove all three limits
exist.
Problem 15
Let
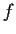
be a holomorphic map of the unit disc
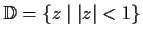
into itself, which is not the identity map
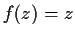
. Show that
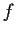
can
have, at most, one fixed point.
Problem 16
Let
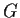
be a group with three normal subgroups
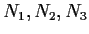
. Suppose
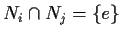
and
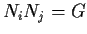
for all
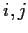
with
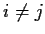
. Show that
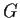
is abelian
and
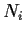
is isomorphic to
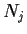
for all
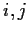
.
Problem 17
Let
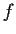
be a continuous function on
![$[0,1]$](img110-10.gif)
. Evaluate the following
limits.
-
-
Problem 18
Let
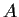
and
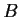
be two real
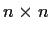
matrices. Suppose there is
a complex invertible
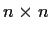
matrix
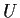
such that
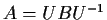
.
Show that there is a real invertible
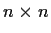
matrix
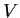
such
that
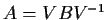
. (In other words, if two real matrices are
similar over
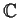
, then they are similar over
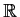
.)
Problem 19
Either prove or disprove (by a counterexample) each of the
following statements:
- Let
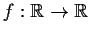 ,
,
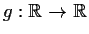 be such that
be such that
Then
- If
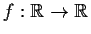 is continuous and
is continuous and 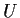 is an open
set in
is an open
set in 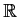 , then
, then 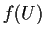 is an open set in
is an open set in 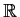 .
.
- Let f be of class
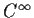 on the interval
on the interval
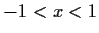 . Suppose that
. Suppose that
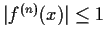 for all
for all
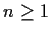 and all x in the interval. Then f is real analytic;
that is, it has a convergent power series expansion in a neighborhood
of each point of the interval. _function,>real analytic
and all x in the interval. Then f is real analytic;
that is, it has a convergent power series expansion in a neighborhood
of each point of the interval. _function,>real analytic
Problem 20
Let
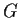
be a group of order
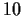
which has a normal subgroup
of order
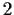
. Prove that
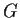
is abelian.



Previous: Summer81
Next: Spring82
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
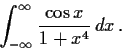



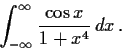
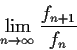
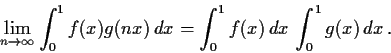
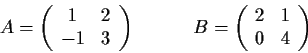
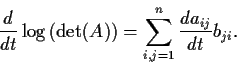
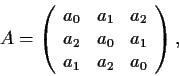
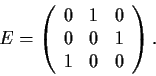
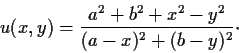
![]() cannot be the real part of an entire function.
Why? Change
cannot be the real part of an entire function.
Why? Change ![]() slightly and do the problem.
slightly and do the problem.