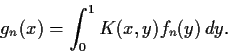Previous: Spring81
Next: Fall81
Preliminary Exam - Summer 1981
Problem 1
Let
Justify the statement
where
Problem 3
Prove or disprove: The set
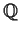
of rational numbers is the intersection of
a countable family of open subsets of
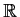
.
Problem 4
Let
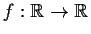
be continuous, with
Show that there is a sequence
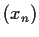
such that
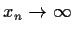
,
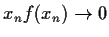
, and
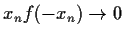
as
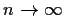
.
Problem 5
Let
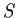
denote the vector space of real
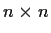
skew-symmetric matrices.
For a nonsingular matrix
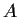
, compute the determinant of the linear map
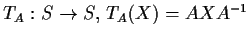
.
Problem 6
Let
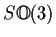
denote the group of orthogonal transformations of
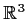
of
determinant
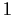
. Let
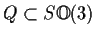
be the subset of symmetric
transformations
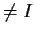
. Let
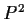
denote the space of lines through
the origin in
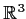
.
- Show that
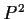 and
and
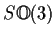 are compact metric spaces (in their
usual topologies).
are compact metric spaces (in their
usual topologies).
- Show that
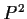 and
and 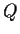 are homeomorphic.
are homeomorphic.
Problem 7
Compute
where
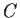
is the circle
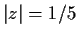
, positively oriented.
Problem 8
Show that
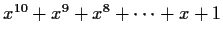
is irreducible over
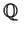
. How about
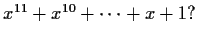
Problem 9
Let
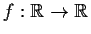
be the function of period
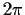
such that
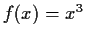
for
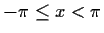
.
- Prove that the Fourier series for
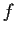 has the form
has the form
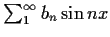 and write an integral formula for
and write an integral formula for 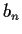 (do
not evaluate it).
(do
not evaluate it).
- Prove that the Fourier series converges for all
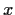 .
.
- Prove
Problem 11
Show that the equation
has, for each sufficiently small
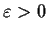
, exactly two solutions. Let
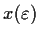
be the smaller one. Show that
- 1.
-
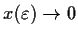 as
as
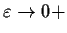 ;
;
yet for any 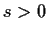 ,
,
- 2.
-
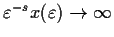 as
as
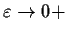 .
.
Problem 12
Show that no commutative ring with identity has additive group isomorphic
to
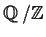
.
Problem 13
Let
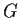
be an additive group, and
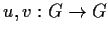
homomorphisms. Show that
the map
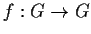
,
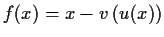
is surjective
if the map
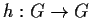
,
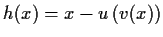
is surjective.
Problem 14
Let
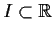
be the open interval from
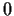
to
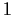
.
Let
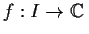
be
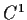
(i.e., the real and imaginary parts are continuously differentiable).
Suppose that
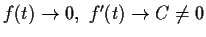
as
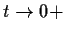
. Show
that the function
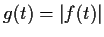
is
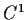
for sufficiently small
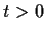
and
that
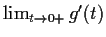
exists, and evaluate the limit.
Problem 15
Let
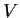
be a finite-dimensional vector space over the rationals
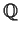
and
let
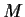
be an automorphism of
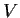
such that
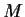
fixes no
nonzero vector in
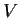
. Suppose that
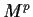
is the identity map on
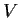
,
where
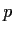
is a prime number. Show that the dimension of
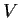
is
divisible by
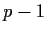
.
Problem 16
Let
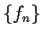
be a sequence of continuous functions
![% latex2html id marker 1137
$[0,1] \to \mbox{$\mathbb{R}^{}$}$](img107-8.gif)
such that
Let
![% latex2html id marker 1141
$K:[0,1] \times [0,1] \to \mbox{$\mathbb{R}^{}$}$](img109-8.gif)
be continuous. Define
![% latex2html id marker 1145
$g_n:[0,1] \to \mbox{$\mathbb{R}^{}$}$](img110-8.gif)
by
Prove that the sequence
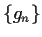
converges uniformly.
Problem 17
Suppose that
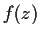
and
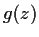
are entire functions such that
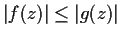
for all
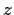
. Show that
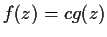
for some
constant
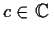
.
Problem 18
Let
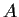
and
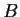
be square matrices of rational numbers such that
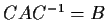
for some real matrix
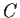
. Prove that such a
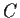
can be chosen to have
rational entries.
Problem 19
Prove that the number of roots of the equation
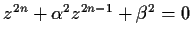
(
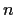
a natural number,
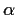
and
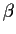
real, nonzero) that have
positive real part is
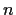 if
if 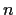 is even, and
is even, and
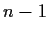 if
if 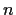 is odd.
is odd.
Problem 20
Let
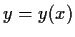
be a solution of the differential equation
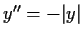
with
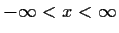
,
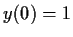
, and
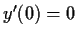
.
- Show that
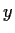 is an even function.
is an even function.
- Show that
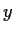 has exactly one zero on the positive real axis.
has exactly one zero on the positive real axis.



Previous: Spring81
Next: Fall81
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
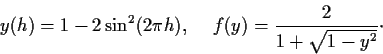
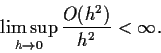



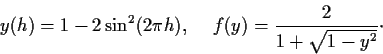
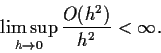
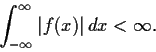
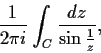
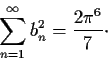
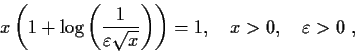
![]() ,
,