


Previous: Fall80
Next: Summer81
Preliminary Exam - Spring 1981
Problem 1
Let
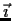
,
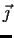
, and
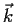
be the usual unit vectors in
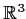
. Let
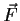
denote the vector field
- Compute
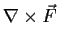 (the curl of
(the curl of 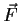 ).
).
- Compute the integral of
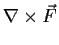 over
the surface
over
the surface
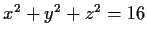 ,
, 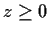 .
.
Problem 2
Let
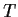
be a linear transformation of a vector space
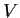
into itself. Suppose
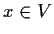
is such that
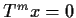
,
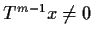
for some positive
integer
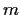
. Show that
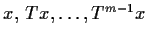
are linearly independent.
Problem 3
Let
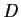
be an ordered integral domain and
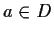
. Prove that
Problem 5
Decompose
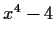
and
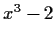
into irreducibles over
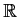
, over
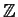
, and
over
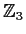
(the integers modulo
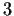
).
Problem 6
Suppose the complex polynomial
has
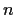
distinct roots
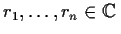
. Prove that if
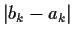
is sufficiently small then
has
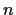
roots which are smooth functions of
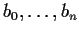
.
Problem 8
Let
![% latex2html id marker 858
$f:[0,1] \to \mbox{$\mathbb{R}^{}$}$](img47-12.gif)
be continuous. Prove that there is a real
polynomial
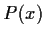
of degree
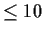
which minimizes (for all such
polynomials)
Problem 9
Show that the following three conditions are all equivalent for a real
3
3 symmetric matrix
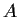
, whose eigenvalues are
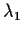
,
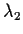
, and
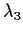
:
-
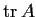 is not an eigenvalue of
is not an eigenvalue of 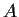 .
.
-
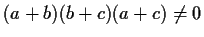 .
.
- The map
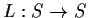 is an isomorphism, where
is an isomorphism, where 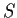 is the space of
3
is the space of
3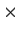 3 real skew-symmetric matrices and
3 real skew-symmetric matrices and
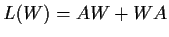 .
.
Problem 11
Evaluate
where
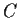
is the closed curve shown below:
file=../Fig/Pr/Sp81-11,width=4.5in
Problem 12
For
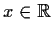
, let
- Prove that
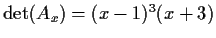 .
.
- Prove that if
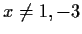 , then
, then
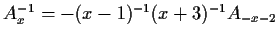 .
.
Problem 13
Which of the following series converges?
-
-
Problem 14
The set of real 3
3 symmetric matrices is a real, finite-dimensional
vector space isomorphic to
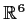
. Show that the subset of such matrices of
signature
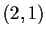
is an open connected subspace in the usual topology on
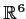
.
Problem 15
Let
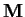
be one of the following fields:
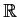
,
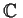
,
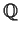
, and
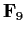
(the field with nine elements).
Let
![% latex2html id marker 1092
$\mathfrak{I} \subset \mbox{\bf {M}}[x]$](img94-11.gif)
be the ideal
generated by
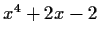
. For which choices of
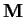
is the
ring
![% latex2html id marker 1098
$\mbox{\bf {M}}[x]/\mathfrak{I}$](img97-11.gif)
a field?
Problem 16
Let
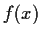
be a real valued function defined for all
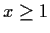
, satisfying
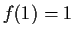
and
Prove that
exists and is less than
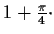
Problem 17
Let b be a real nonzero
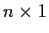
matrix (a column vector). Set
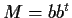
(an
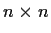
matrix) where
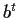
denotes the transpose of b.
- Prove that there is an orthogonal matrix
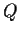 such that
such that 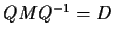 is diagonal, and find
is diagonal, and find 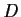 .
.
- Describe geometrically the linear transformation
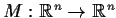 .
.
Problem 18
Describe the two regions in
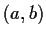
-space for which the function
restricted to the circle
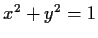
, has exactly two, and exactly four
critical points, respectively.
Problem 19
Let
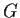
be a finite group. A conjugacy class is a set of the form
for some
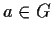
.
- Prove that the number of elements in a conjugacy class divides the
order of
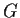 .
.
- Do all conjugacy classes have the same number of elements?
- If
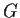 has only two conjugacy classes, prove
has only two conjugacy classes, prove 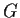 has order
has order 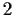 .
.
Problem 20
Let
![% latex2html id marker 1242
$f:[0,1] \to \mbox{$\mathbb{R}^{}$}$](img122-4.gif)
be continuous with
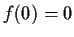
. Show there is a
continuous concave function
![% latex2html id marker 1248
$g:[0,1] \to \mbox{$\mathbb{R}^{}$}$](img124-3.gif)
such that
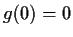
and
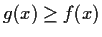
for all
![$x \in [0,1]$](img127-3.gif)
.
Note: A function
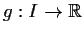 is concave if
is concave if
for all
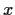
and
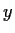
in
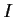
and
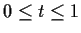
.
_function,>concave



Previous: Fall80
Next: Summer81
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
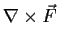 (the curl of
(the curl of 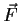 ).
).
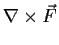 over
the surface
over
the surface
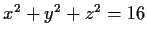 ,
, 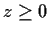 .
.



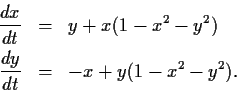
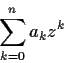
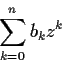
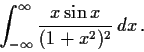
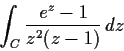
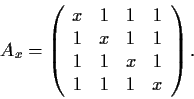
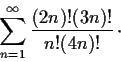
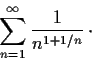
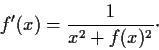
![]() is concave if
is concave if


