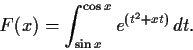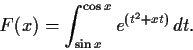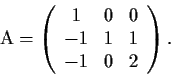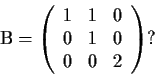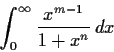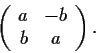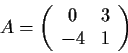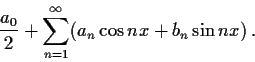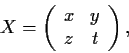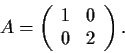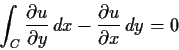Previous: Summer80
Next: Spring81
Preliminary Exam - Fall 1980
Problem 1
Define
Compute
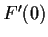
.
Problem 2
Let
Is
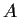
similar to
Problem 3
Do there exist functions
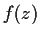
and
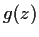
that are analytic at
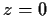
and
that satisfy
-
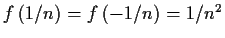 ,
,
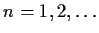 ,
,
-
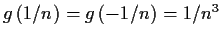 ,
,
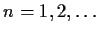 ?
?
Problem 5
Evaluate
where
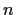
and
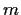
are positive integers and
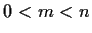
.
Problem 6
Let
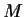
be the ring of real 2
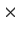
2 matrices and
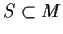
the
subring of matrices of the form
- Exhibit (without proof) an isomorphism between
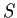 and
and
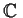 .
.
- Prove that
lies in a subring isomorphic to 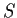 .
.
- Prove that there is an
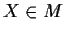 such that
such that 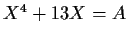 .
.
Problem 7
Let
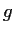
be
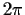
-periodic, continuous on
![$[-\pi,\pi]$](img43-11.gif)
and have Fourier series
Let
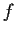
be
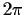
-periodic and satisfy the differential equation
where
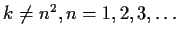
.
Find the Fourier series of
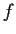
and prove that it converges everywhere.
Problem 8
Let
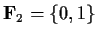
be the field with two elements. Let
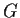
be the group
of invertible 2
2 matrices with entries in
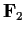
. Show that
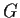
is isomorphic to
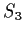
, the group of permutations of three objects.
Problem 9
For a real 2
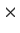
2 matrix
let
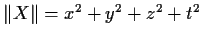
, and define a metric by
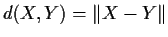
. Let
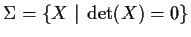
. Let
Find the minimum distance from
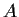
to
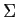
and exhibit an
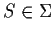
that achieves this minimum.
Problem 10
Show that there is an
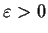
such that if
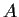
is any real 2
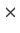
2 matrix satisfying
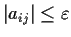
for all entries
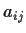
of
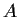
, then there is a real 2
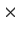
2 matrix
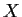
such that
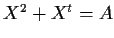
,
where
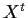
is the transpose of
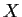
. Is
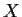
unique?
Problem 11
Let
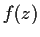
be an analytic function defined for
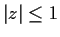
and let
Prove that
where
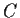
is the unit circle,
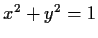
.
Problem 12
Prove that any group of order
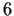
is isomorphic to either
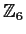
or
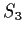
(the group of permutations of three objects).
Problem 13
Let
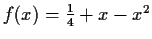
. For any real number
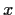
, define a sequence
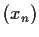
by
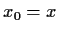
and
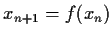
. If the sequence converges, let
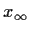
denote the limit.
- For
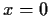 , show that the sequence is bounded and nondecreasing and
find
, show that the sequence is bounded and nondecreasing and
find
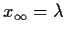 .
.
- Find all
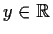 such that
such that
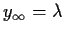 .
.
Problem 14
Exhibit a set of 2
2 real matrices with the following
property: A matrix
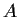
is similar to exactly one matrix in
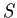
provided
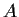
is a 2
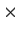
2 invertible matrix of integers with all the roots of
its characteristic polynomial on the unit circle.
Problem 15
Consider the differential equation
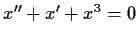
and the function
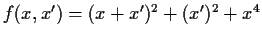
.
- Show that
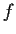 decreases along trajectories of the differential
equation.
decreases along trajectories of the differential
equation.
- Show that if
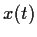 is any solution, then
is any solution, then 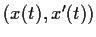 tends to
tends to
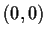 as
as 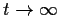 .
.
Problem 16
Suppose that
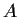
and
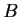
are real matrices such that
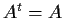
,
for all
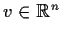
and
Show that
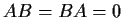
and give an example where neither
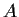
nor
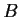
is zero.
Problem 17
Let
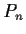
be a sequence of real polynomials of degree
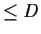
, a fixed
integer. Suppose that
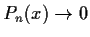
pointwise for
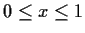
.
Prove that
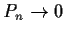
uniformly on
![$[0,1]$](img122-3.gif)
.
Problem 18
Suppose that
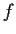
is analytic inside and on the unit circle
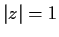
and
satisfies
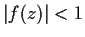
for
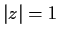
. Show that the equation
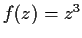
has exactly three solutions (counting multiplicities) inside the unit
circle.
Problem 19
Let
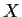
be a compact metric space and
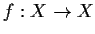
an isometry.
Show that
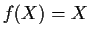
.
Problem 20
Let
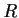
be a ring with multiplicative identity
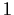
. Call
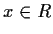
a
unit if
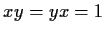
for some
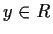
. Let
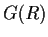
denote the set of units. _ring>unit
- Prove
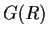 is a multiplicative group.
is a multiplicative group.
- Let
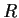 be the ring of complex numbers
be the ring of complex numbers 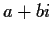 , where
, where 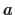 and
and 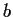 are
integers. Prove
are
integers. Prove 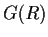 is isomorphic to
is isomorphic to
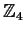 (the additive group
of integers modulo
(the additive group
of integers modulo 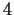 ).
).



Previous: Summer80
Next: Spring81
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10