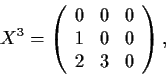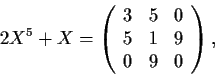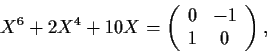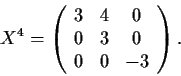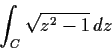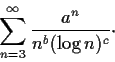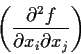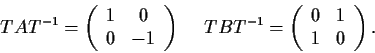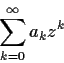Previous: Spring80
Next: Fall80
Preliminary Exam - Summer 1980
Problem 1
Exhibit a real 3
3 matrix having minimal polynomial
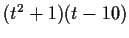
, which, as a linear transformation of
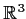
,
leaves invariant the line
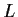
through
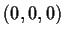
and
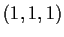
and the plane
through
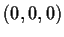
perpendicular to
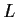
.
Problem 2
Which of the following matrix equations have a real matrix solution X?
(It is not necessary to exhibit solutions.)
-
-
-
-
Problem 3
Let
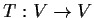
be an invertible linear transformation of a vector
space
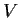
. Denote by
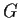
the group of all maps
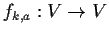
where
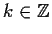
,
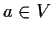
, and for
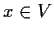
,
Prove that the commutator subgroup
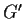
of
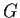
is isomorphic to the
additive group of the vector space
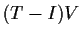
, the image of
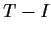
.
(
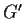
is generated by all
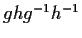
,
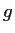
and
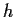
in
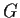
.)
Problem 5
Consider the differential equations
Let
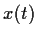
and
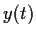
be a solution defined for all
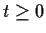
with
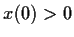
and
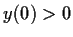
. Prove that
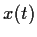
and
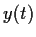
are bounded.
Problem 6
Let
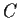
denote the positively oriented circle
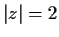
,
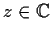
. Evaluate the integral
where the branch of the square root is chosen so that
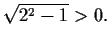
Problem 7
Exhibit a conformal map from the set
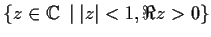
onto
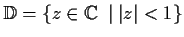
.
Problem 8
Give an example of a subset of
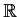
having uncountably many connected
components. Can such a subset be open? Closed?
Problem 9
For each
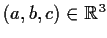
, consider the series
Determine the values of
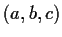
for which the series
- converges absolutely;
- converges but not absolutely;
- diverges.
Problem 10
Let
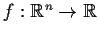
be a function whose partial derivatives of
order
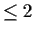
are everywhere defined and continuous.
- Let
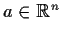 be a critical point of f (i.e.,
be a critical point of f (i.e.,
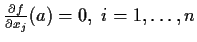 ).
Prove that a is a local minimum provided the Hessian matrix
).
Prove that a is a local minimum provided the Hessian matrix
is positive definite at 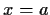 .
.
- Assume the Hessian matrix is positive definite at all x.
Prove that f has, at most, one critical point.
Problem 11
Prove that every finite group is isomorphic to
- A group of permutations;
- A group of even permutations.
Problem 12
Let
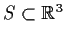
denote the ellipsoidal surface defined by
Let
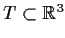
be the surface
defined by
Prove that there exist points
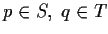
, such that the line
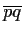
is
perpendicular to
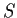
at
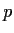
and to
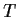
at
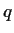
.
Problem 13
Let
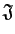
be the ideal in the ring
![% latex2html id marker 1054
$\mbox{$\mathbb{Z}^{}$}[x]$](img77-10.gif)
(of polynomials with integer
coefficients) generated by
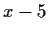
and
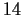
. Find
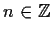
such
that
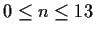
and
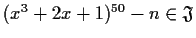
.
Problem 14
Let
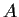
and
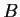
be real 2
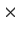
2 matrices with
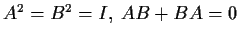
. Prove there exists a real nonsingular matrix
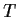
with
Problem 15
Let
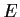
be a finite-dimensional vector space over a field
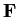
. Suppose
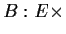
E
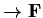
is a bilinear map (not necessarily symmetric).
Define subspaces
Prove that
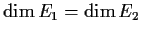
.
Problem 16
Let
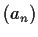
be a sequence of nonzero real numbers. Prove that the
sequence of functions
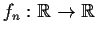
has a subsequence converging to a continuous function.
Problem 17
Let
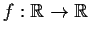
be monotonically increasing (perhaps
discontinuous). Suppose
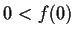
and
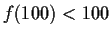
. Prove
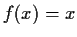
for some
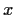
.
Problem 18
How many zeros does the complex polynomial
have in the annulus
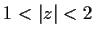
?
Problem 19
Let
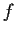
be a meromorphic function on
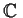
which is analytic in a
neighborhood of
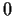
. Let its Maclaurin series be
with all
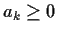
. Suppose there is a pole of modulus
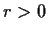
and no pole has modulus
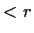
. Prove there is a pole at
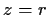
.
Problem 20
Prove that the initial value problem
has a solution
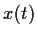
defined for all
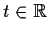
.



Previous: Spring80
Next: Fall80
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10