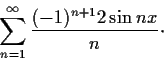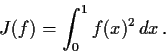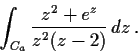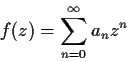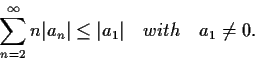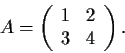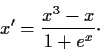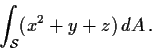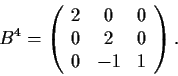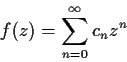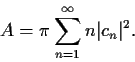Previous: Fall79
Next: Summer80
Preliminary Exam - Spring 1980
Problem 1
Let
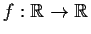
be the unique function such that
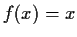
if
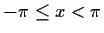
and
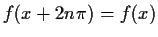
for all
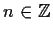
.
- Prove that the Fourier series of
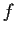 is
is
- Prove that the series does not converge uniformly.
- For each
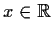 , find the sum of the series.
, find the sum of the series.
Problem 2
Let
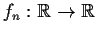
be differentiable for each n = 1, 2, ...
with
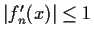
for all n, x. Assume
for all x. Prove that
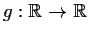
is continuous.
Problem 3
Let
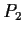
denote the set of real polynomials of degree
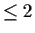
.
Define the map
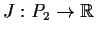
by
Let
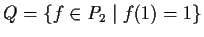
. Show that
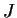
attains
a minimum value on
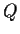
and determine where the minimum occurs.
Problem 4
Let
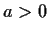
be a constant
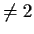
. Let
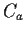
denote the positively
oriented circle of radius
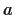
centered at the origin. Evaluate
Problem 5
Let
be an analytic function in the open unit disc
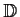
.
Assume that
Prove that
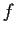
is injective.
Problem 6
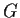
is a group of order
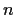
,
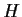
a proper subgroup of order
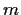
,
and
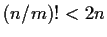
. Prove
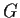
has a proper normal subgroup different
from the identity.
Problem 7
Let
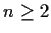
be an integer such that
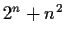
is prime. Prove
that
Problem 9
Let
Show that every real matrix
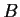
such that
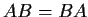
has the form
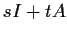
, where
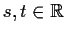
.
Problem 10
Consider the differential equation
- Find all its constant solutions.
- Discuss
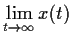 , where
, where 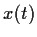 is
the solution such that
is
the solution such that
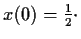
Problem 11
Let
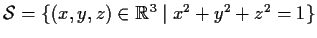
denote the
unit sphere in
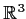
. Evaluate the surface integral over S:
Problem 12
Let
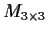
denote the vector space of real 3
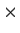
3 matrices.
For any matrix
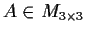
, define the linear operator
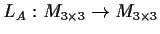
,
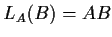
.
Suppose that the determinant of
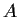
is
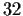
and the minimal polynomial is
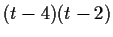
.
What is the trace of
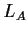
?
Problem 13
Let
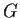
be a group of permutations of a set
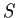
of
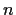
elements. Assume
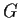
is
transitive; that is, for any
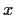
and
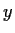
in
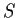
, there is some
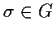
with
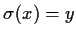
. _group of permutations,>transitive
- Prove that
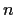 divides the order of
divides the order of 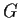 .
.
- Suppose
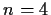 . For which integers
. For which integers 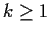 can such a
can such a 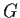 have
order
have
order 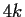 ?
?
Problem 14
Find a real matrix
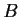
such that
Problem 15
Show that a vector space over an infinite field cannot be the
union of a finite number of proper subspaces.
Problem 16
Let
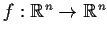
be continuously differentiable. Assume the
Jacobian matrix
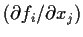
has rank n everywhere.
Suppose

is
proper; that is,
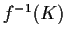
is compact whenever
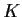
is compact. Prove
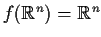
. _function,>proper
Problem 17
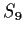
is the group of permutations of the set of integers from
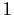
to
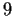
.
- Exhibit an element of
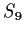 of order
of order 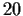 .
.
- Prove that no element of
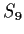 has order
has order 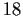 .
.
Problem 18
For each
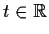
, let
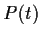
be a symmetric real
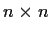
matrix whose entries are continuous functions of
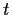
. Suppose for
all
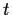
that the eigenvalues of
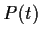
are all
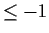
. Let
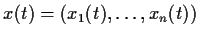
be a solution of the vector
differential equation
Prove that
Problem 19
Let
be analytic in the disc
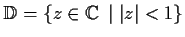
.
Assume
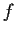
maps
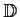
one-to-one onto a domain
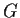
having area
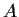
. Prove
Problem 20
Does there exist an analytic function mapping the annulus
onto the annulus
and taking
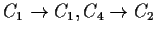
, where
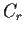
is the
circle of radius r?



Previous: Fall79
Next: Summer80
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
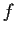 is
is
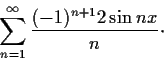
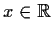 , find the sum of the series.
, find the sum of the series.