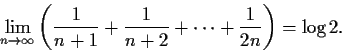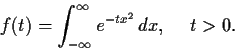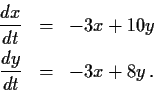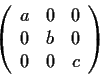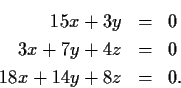Previous: Summer79
Next: Spring80
Preliminary Exam - Fall 1979
Problem 1
Prove that the polynomial
has at least one root in the disc

.
Problem 2
Suppose that
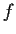
is analytic on the open upper half-plane and
satisfies
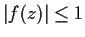
for all

,
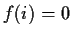
. How large can
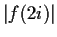
be under these conditions?
Problem 3
Prove that every finite group of order
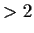
has a nontrivial
automorphism.
Problem 4
Consider the polynomial ring
![% latex2html id marker 702
$\mbox{$\mathbb{Z}^{}$}[x]$](img9-8.gif)
and the ideal
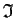
generated by
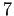
and
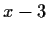
.
- Show that for each
![% latex2html id marker 712
$r \in \mbox{$\mathbb{Z}^{}$}[x]$](img13-8.gif) , there is an integer
, there is an integer 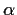 satisfying
satisfying
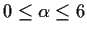 such that
such that
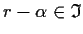 .
.
- Find
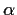 in the special case
in the special case
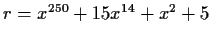 .
.
Problem 5
Let
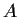
be a real
skew-symmetric matrix
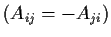
. Prove that
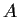
has even rank.
_matrix,>skew-symmetric
Problem 6
Let
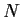
be a linear operator on an

-dimensional vector space,
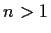
,
such that
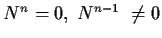
. Prove there is no operator
X with
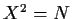
.
Problem 9
Given that
find
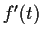
explicitly, where
Problem 10
Solve the differential equations
Problem 11
An accurate map of California is spread out flat on a table in Evans Hall,
in Berkeley. Prove that there is exactly one point on the map lying directly
over the point it represents.
Problem 12
Consider the following properties of a map
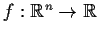
:
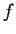 is continuous.
is continuous.
- The graph of
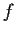 is connected in
is connected in
 .
.
Prove or disprove the implications 1
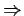
2, 2
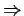
1.
Problem 13
Let
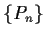
be a sequence of real polynomials of degree
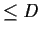
, a fixed
integer. Suppose that
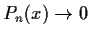
pointwise for
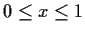
.
Prove that
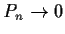
uniformly on
![$[0,1]$](img59-8.gif)
.
Problem 14
Let
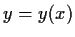
be a solution of the differential equation
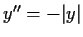
with
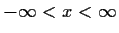
,
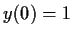
and
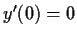
.
- Show that
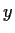 is an even function.
is an even function.
- Show that
 has exactly one zero on the positive real axis.
has exactly one zero on the positive real axis.
Problem 15
Suppose
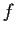
and
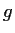
are entire functions with

for all
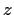
. Prove that

for
some constant
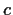
.
Problem 16
Prove that
What restrictions must be placed on
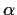
?
Problem 17
Let

be an
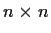
complex matrix. Prove there is a unitary
matrix
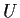
such that
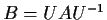
is upper-triangular:
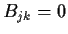
for
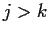
.
Problem 18
Let
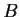
denote the matrix
where
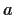
,
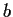
, and
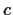
are real and

,
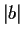
, and
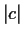
are distinct. Show that there are exactly four symmetric
matrices of the form
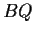
, where

is a real orthogonal matrix
of determinant

.
Problem 19
Let
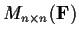
be the ring of
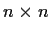
matrices over a field
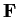
. Prove that it has no 2-sided ideals except
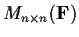
and
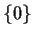
.
Problem 20
Let
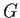
be the abelian group defined by generators
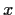
,
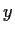
, and
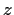
, and
relations
- Express
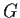 as a direct product of two cyclic groups.
as a direct product of two cyclic groups.
- Express
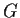 as a direct product of cyclic groups of prime
power order.
as a direct product of cyclic groups of prime
power order.
- How many elements of
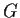 have order
have order 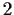 ?
?



Previous: Summer79
Next: Spring80
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10