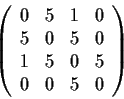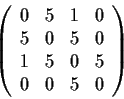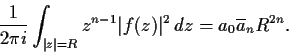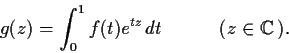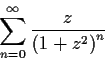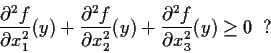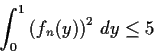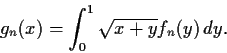Previous: Spring79
Next: Fall79
Preliminary Exam - Summer 1979
Problem 1
Prove that the matrix
has two positive and two negative eigenvalues (counting
multiplicities).
Problem 2
Let
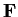
be a subfield of a field
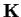
. Let
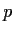
and
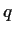
be
polynomials over
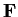
. Prove that their
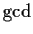
(greatest common
divisor) in the ring of polynomials over
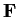
is the same as their
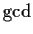
in the ring of polynomials over
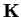
.
Problem 3
Let
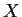
be the space of orthogonal real
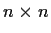
matrices. Let
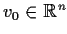
. Locate and describe the elements of
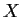
, where the map
takes its maximum and minimum values.
Problem 4
Prove that the group of automorphisms of a cyclic group of
prime order
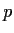
is cyclic and find its order.
Problem 6
Let
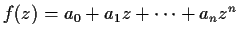
be a complex polynomial
of degree
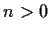
. Prove
Problem 7
Let
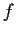
be a continuous complex valued function on
![$[0,1]$](img27-7.gif)
, and
define the function
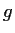
by
Prove that
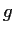
is analytic in the entire complex plane.
Problem 8
Let
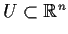
be an open set. Suppose that the map
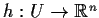
is a homeomorphism from
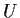
onto
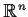
, which is
uniformly continuous. Prove

.
Problem 9
Prove that a linear transformation
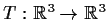
has
- a one-dimensional invariant subspace, and
- a two-dimensional invariant subspace.
Problem 10
Find real valued functions of a real variable,
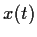
,
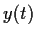
, and
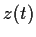
, such that
and
Problem 11
Let
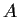
and
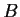
be
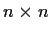
matrices over a field
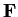
such that
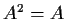
and
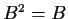
. Suppose that
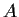
and
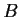
have the same
rank. Prove that
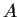
and
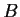
are similar.
Problem 12
Which rational numbers
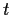
are such that
is an integer?
Problem 14
Let
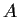
,
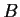
, and
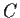
be finite abelian groups such that A
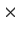
B and
A
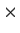
C are isomorphic. Prove that
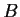
and
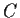
are isomorphic.
Problem 15
Show that
converges for all complex numbers
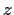
exterior to the
lemniscate
Problem 16
Let
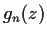
be an entire function having only real zeros,
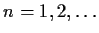
. Suppose
uniformly on compact sets in
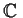
, with
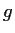
not identically zero.
Prove that
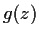
has only real zeros.
Problem 17
Let
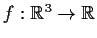
be such that
Suppose
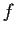
has continuous partial derivatives of orders
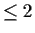
.
Is there a
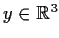
with
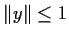
such that
Problem 18
Let
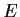
be a three-dimensional vector space over
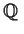
. Suppose
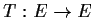
is a linear transformation and
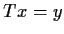
,
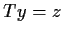
,
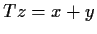
, for certain
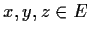
,
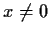
. Prove that
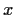
,
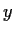
, and
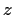
are linearly independent.
Problem 19
Let
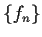
be a sequence of continuous functions
![% latex2html id marker 1208
$[0,1] \to \mbox{$\mathbb{R}^{}$}$](img103-4.gif)
such that
for all n.
Define
![% latex2html id marker 1212
$g_n:[0,1] \to\mbox{$\mathbb{R}^{}$}$](img105-3.gif)
by
- Find a constant
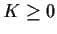 such that
such that
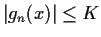 for all n.
for all n.
- Prove that a subsequence of the sequence {
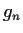 } converges
uniformly.
} converges
uniformly.
Problem 20
Let
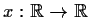
be a solution to the differential equation
Prove that the function
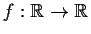
,
attains a maximum value.



Previous: Spring79
Next: Fall79
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10