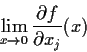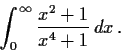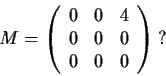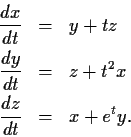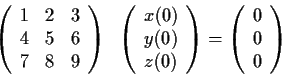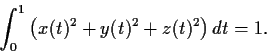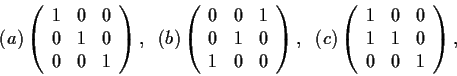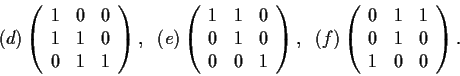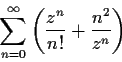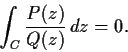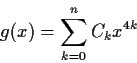Previous: Fall78
Next: Summer79
Preliminary Exam - Spring 1979
Problem 1
Let
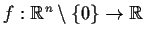
be differentiable. Suppose
exists for each
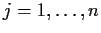
.
- Can
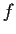 be extended to a continuous map from
be extended to a continuous map from
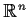 to
to 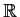 ?
?
- Assuming continuity at the origin, is
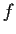 differentiable
from
differentiable
from
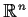 to
to 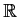 ?
?
Problem 3
Let
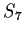
be the group of permutations of a set of seven elements.
Find all
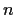
such that some element of
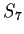
has order
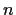
.
Problem 4
Prove that every compact metric space has a countable dense subset.
Problem 5
Find all solutions to the differential equation
Problem 6
Prove that if
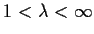
, the function
has only one zero in the half-plane
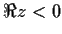
, and that this zero is real.
Problem 8
Let
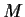
be a real nonsingular 3
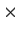
3 matrix. Prove there are
real matrices
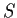
and
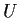
such that
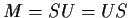
, all the eigenvalues
of
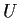
equal
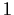
, and
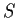
is diagonalizable over
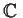
.
Problem 9
Let
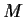
be an
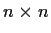
complex matrix. Let
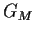
be the set of complex
numbers
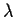
such that the matrix
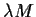
is similar to
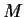
.
- What is
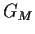 if
if
- Assume
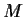 is not nilpotent. Prove
is not nilpotent. Prove 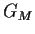 is finite.
is finite.
Problem 10
Let
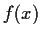
be a polynomial over
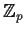
, the field of integers

. Let
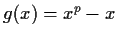
. Show that the greatest
common divisor of
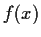
and
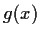
is the product of the distinct
linear factors of
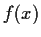
.
Problem 11
Let
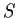
be a collection of abelian groups, each of order
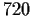
, no two
of which are isomorphic. What is the maximum cardinality
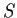
can have?
Problem 12
Let
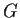
be a group with three normal subgroups
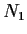
,
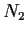
, and
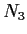
. Suppose
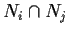
= {e} and
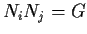
for all
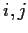
with
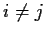
. Show that
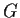
is abelian and
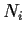
is isomorphic to
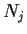
for all
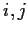
.
Problem 13
Consider the system of differential equations:
Prove there exists a solution defined for all
![$t \in [0,1]$](img70-6.gif)
,
such that
and also
Problem 15
Which of the following matrices are similar as matrices over
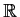
?
Problem 16
For which
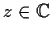
does
converge?
Problem 17
Let
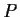
and
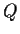
be complex polynomials with the degree of
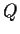
at least two
more than the degree of
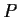
. Prove there is an
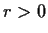
such that if
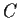
is a closed curve outside
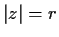
, then
Problem 18
Show that for any continuous function
![% latex2html id marker 1130
$f:[0,1] \to
\mbox{$\mathbb{R}^{}$}$](img96-5.gif)
and
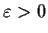
, there is a function of the form
for some
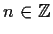
, where
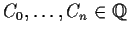
and
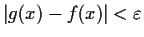
for all x in
![$[0,1]$](img102-5.gif)
.
Problem 19
Let
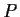
be a 9
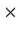
9 real matrix such that
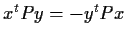
for all column vectors
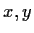
in
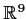
.
Prove that
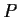
is singular.



Previous: Fall78
Next: Summer79
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
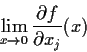
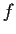 be extended to a continuous map from
be extended to a continuous map from
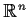 to
to 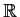 ?
?
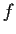 differentiable
from
differentiable
from
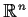 to
to 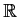 ?
?