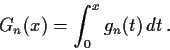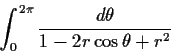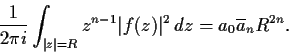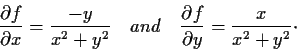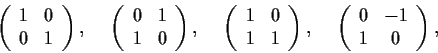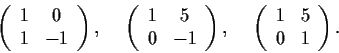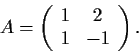Previous: Summer78
Next: Spring79
Preliminary Exam - Fall 1978
Problem 1
Let
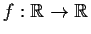
satisfy
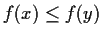
for
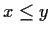
. Prove
that the set where
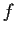
is not continuous is finite or countably infinite.
Problem 2
Let
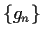
be a sequence of Riemann integrable functions from
![$[0,1]$](img6-4.gif)
into
such that
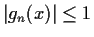
for all
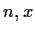
.
Define
Prove that a subsequence of
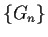
converges uniformly.
Problem 3
Let
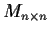
denote the vector space of
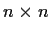
real matrices
(identified with
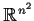
). Prove that there are neighborhoods
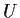
and
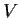
in
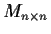
of the identity matrix such that for every
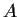
in
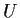
,
there is a unique
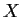
in
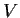
such that
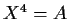
.
Problem 4
Evaluate
where
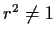
.
Problem 5
Let
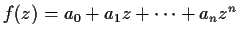
be a complex polynomial
of degree
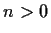
. Prove
Problem 6
Solve the differential equation
Problem 7
Let
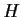
be a subgroup of a finite group
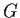
.
- Show that
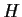 has the same number of left cosets as
right cosets.
has the same number of left cosets as
right cosets.
- Let
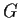 be the group of symmetries of the square. Find
a subgroup
be the group of symmetries of the square. Find
a subgroup 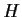 such that xH
such that xH 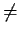 Hx for some x.
Hx for some x.
Problem 9
For
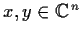
, let
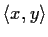
be the Hermitian inner product
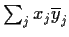
. Let
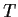
be a linear operator
on
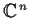
such that
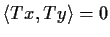
if
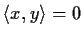
. Prove
that
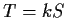
for some scalar
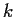
and some operator
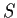
which is
unitary:
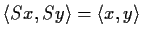
for all
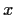
and
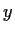
.
_matrix,>unitary
Problem 10
How many homomorphisms are there from the group
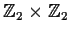
to the symmetric group on three letters?
Problem 11
Let
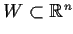
be an open connected set and
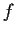
a real valued
function on
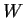
such that all partial derivatives of
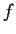
are
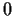
. Prove
that
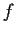
is constant.
Problem 12
Let
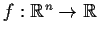
have the following properties:
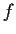
is
differentiable on

,
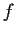
is continuous at
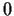
,
and
for
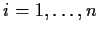
. Prove that
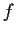
is differentiable at
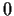
.
Problem 15
Suppose
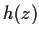
is analytic in the whole plane,
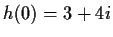
, and
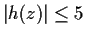
if
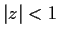
. What is
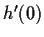
?
Problem 16
Which pairs of the following matrices are similar?
Problem 17
Find all automorphisms of the additive group of rational numbers.
Problem 18
Prove that every finite multiplicative group of complex numbers is cyclic.
Problem 19
Let
Express
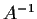
as a polynomial in
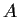
with real coefficients.
Problem 20
Let
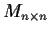
be the vector space of real
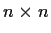
matrices, identified with
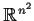
. Let
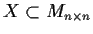
be a compact set. Let
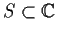
be
the set of all numbers that are eigenvalues of at least one element of
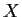
.
Prove that
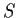
is compact.



Previous: Summer78
Next: Spring79
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10