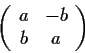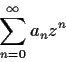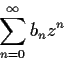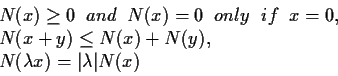Previous: Spring78
Next: Fall78
Preliminary Exam - Summer 1978
Problem 1
For each of the following either give an example
or else prove that no such example is possible.
- A nonabelian group.
- A finite abelian group that is not cyclic.
- An infinite group with a subgroup of index
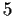 .
.
- Two finite groups that have the same order but
are not isomorphic.
- A group
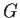 with a subgroup
with a subgroup 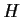 that is not normal.
that is not normal.
- A nonabelian group with no normal subgroups except
the whole group and the unit element.
- A group
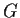 with a normal subgroup
with a normal subgroup 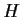 such that the
factor group
such that the
factor group 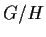 is not isomorphic to any subgroup of
is not isomorphic to any subgroup of 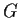 .
.
- A group
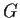 with a subgroup
with a subgroup  which has index
which has index 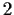 but
is not normal.
but
is not normal.
Problem 2
Let
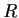
be the set of 2
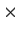
2 matrices of the form
where a, b are elements of a given field
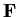
. Show that with
the usual matrix operations,
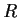
is a commutative ring
with identity. For which of the following fields
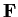
is
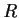
a field:
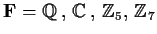
?
Problem 6
Let
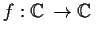
be an entire function and let
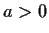
and
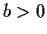
be constants.
- If
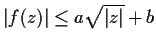 for all z, prove
that f is a constant.
for all z, prove
that f is a constant.
- What can you prove about f if
for all z?
Problem 8
Let
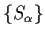
be a family of connected subsets of

all
containing the origin. Prove that
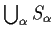
is connected.
Problem 9
Let
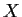
and
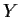
be nonempty subsets of a metric space
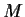
. Define
- Suppose
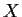 contains only one point
contains only one point 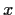 , and
, and 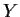 is closed. Prove
is closed. Prove
for some 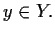
- Suppose
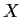 is compact and
is compact and 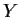 is closed. Prove
is closed. Prove
for some
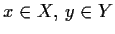 .
.
- Show by example that the conclusion of Part 2 can be false
if
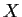 and
and 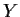 are closed but not compact.
are closed but not compact.
Problem 10
Let
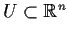
be a convex open set and
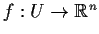
a
differentiable function whose partial derivatives are uniformly bounded
but not necessarily continuous. Prove that f has a unique continuous
extension to the closure of
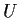
.
Problem 11
Suppose the power series
converges for

R where
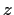
and the
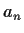
are complex numbers. If
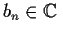
are such that
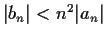
for all
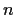
, prove that
converges for

R.
Problem 12
- Suppose f is analytic on a connected open set
 and f takes only real values. Prove that f is constant.
and f takes only real values. Prove that f is constant.
- Suppose
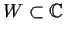 is open, g is analytic on
is open, g is analytic on 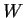 , and
, and
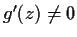 for all
for all 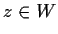 . Show that
. Show that
is an open subset of  .
.
Problem 13
Let
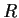
denote the ring of polynomials over a field
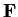
. Let
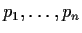
be elements of

. Prove that the greatest
common divisor of
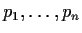
is
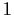
if and only if there
is an
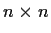
matrix over
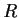
of determinant
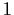
whose first
row is
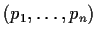
.
Problem 14
Let
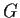
be a finite multiplicative group of 2
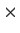
2 integer matrices.
- Let
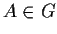 . What can you prove about
. What can you prove about
- (i)
 ?
?
- (ii)
- the (real or complex) eigenvalues of A?
- (iii)
- the Jordan or Rational Canonical Form of A?
- (iv)
- the order of A?
- Find all such groups up to isomorphism.
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 15
Let
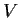
be a finite-dimensional vector space over an algebraically
closed field. A linear operator

is called completely
reducible if whenever a linear subspace

is invariant
under

(i.e.,
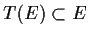
), there is a linear subspace
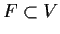
which is invariant under
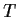
and such that
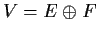
.
Prove that
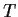
is completely reducible if and only if
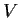
has a basis of
eigenvectors.
Problem 18
Let
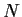
be a
norm on the vector space
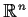
; that is,
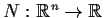
satisfies _norm
for all
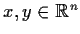
and
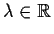
.
- Prove that
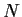 is bounded on the unit sphere.
is bounded on the unit sphere.
- Prove that
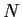 is continuous.
is continuous.
- Prove that there exist constants
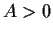 and
and 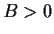 , such that for
all
, such that for
all
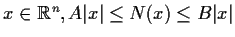 .
.
Problem 19
Let
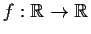
be continuous. Suppose that
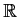
contains a
countably infinite subset
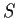
such that
if
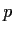
and
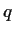
are not in
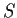
. Prove that

is identically
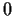
.
Problem 20
Let
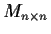
denote the vector space of real n

n matrices.
Define a map
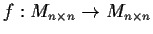
by

.
Find the derivative of

.



Previous: Spring78
Next: Fall78
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
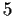 .
.
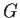 with a subgroup
with a subgroup 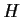 that is not normal.
that is not normal.
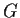 with a normal subgroup
with a normal subgroup 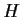 such that the
factor group
such that the
factor group 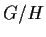 is not isomorphic to any subgroup of
is not isomorphic to any subgroup of 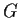 .
.
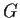 with a subgroup
with a subgroup  which has index
which has index 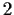 but
is not normal.
but
is not normal.