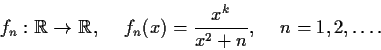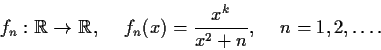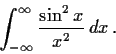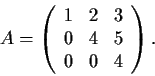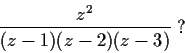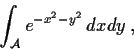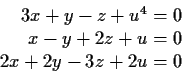Previous: Fall77
Next: Summer78
Preliminary Exam - Spring 1978
Problem 1
Let
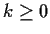
be an integer and define a sequence of maps
For which values of
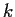
does the sequence converge uniformly on
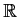
? On every bounded subset of
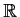
?
Problem 2
Prove that a map
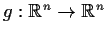
is continuous only if its graph
is closed in
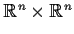
. Is the converse true?
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 3
Let
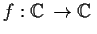
be a nonconstant entire function.
Prove that
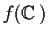
is dense in
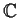
.
Problem 5
let
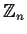
denote the ring of integers modulo n. Let
![% latex2html id marker 829
$\mbox{$\mathbb{Z}^{}$}_n[x]$](img13-2.gif)
be the ring of polynomials with coefficients in
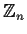
. Let
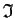
denote the ideal in
![% latex2html id marker 839
$\mbox{$\mathbb{Z}^{}$}_n [x]$](img16-2.gif)
generated by
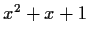
.
- For which values of n,
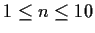 , is the quotient
ring
, is the quotient
ring
![% latex2html id marker 847
$\mbox{$\mathbb{Z}^{}$}_n [x]/\mathfrak{I}$](img19-2.gif) a field?
a field?
- Give the multiplication table for
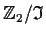 .
.
Problem 6
Prove that the sum of two algebraic numbers is algebraic. (An
algebraic number is a complex number which is a root of a polynomial
with rational coefficients.)
Problem 7
What is the volume enclosed by the ellipsoid
Problem 9
Determine the Jordan Canonical Form of the matrix
Problem 10
Suppose
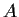
is a real
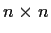
matrix.
- Is it true that
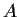 must commute with its transpose?
must commute with its transpose?
- Suppose the columns of
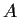 (considered as vectors) form
an orthonormal set; is it true that the rows of
(considered as vectors) form
an orthonormal set; is it true that the rows of 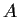 must also
form an orthonormal set?
must also
form an orthonormal set?
Problem 11
Show that there is a complex analytic function defined on the set
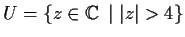
whose derivative is
Is there a complex analytic function on
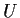
whose derivative is
Problem 12
Prove that the uniform limit of a sequence of complex analytic
functions is complex analytic. Is the analogous theorem true for
real analytic functions?
Problem 13
- For which real numbers
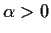 does the differential
equation
does the differential
equation
have a solution on some interval ![$[0,b],\; b>0$](img40-2.gif) ?
?
- For which values of
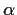 are there intervals on which
two solutions of
are there intervals on which
two solutions of 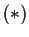 are defined?
are defined?
Problem 14
Let
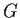
be a group of order
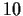
which has a normal subgroup of order
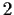
.
Prove that
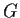
is abelian.
Problem 15
Is
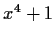
irreducible over the field of real numbers? The field
of rational numbers? A field with
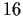
elements?
Problem 16
Let
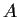
and
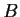
denote real n
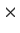
n symmetric matrices such that
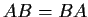
.
Prove that
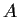
and
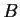
have a common eigenvector in
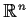
.
Problem 17
Evaluate
where
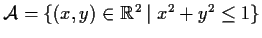
.
Problem 18
Let
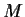
be a matrix with entries in a field
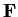
. The
row rank of
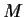
over
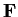
is the maximal number of rows which are linearly independent
(as vectors) over
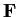
. The
column rank is similarly defined using
columns instead of rows. _matrix,>row rank _matrix,>column rank
- Prove row rank = column rank.
- Find a maximal linearly independent set of columns of
taking
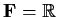 .
.
- If
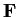 is a subfield of
is a subfield of
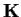 , and
, and 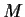 has entries
in
has entries
in
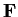 , how is the row rank of
, how is the row rank of 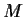 over
over
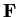 related to the
row rank of
related to the
row rank of 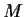 over
over
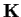 ?
?
Problem 19
Let
![% latex2html id marker 1175
$f:[0,1] \to \mbox{$\mathbb{R}^{}$}$](img73-2.gif)
be Riemann integrable over
![$[b,1]$](img74-2.gif)
for
all b such that
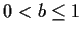
.
- If f is bounded, prove that f is Riemann integrable over
![$[0,1]$](img76-2.gif) .
.
- What if f is not bounded?



Previous: Fall77
Next: Summer78
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10