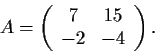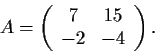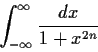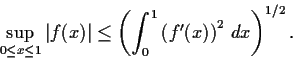Previous: Summer77
Next: Spring78
Preliminary Exam - Fall 1977
Problem 1
Let
Find a real matrix
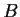
such that
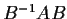
is diagonal.
Problem 3
Let
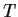
be an
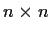
complex matrix. Show that
if and only if all the eigenvalues of
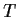
have absolute value
less than
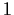
.
Problem 4
Let
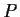
be a linear operator on a finite-dimensional vector space over
a finite field. Show that if
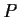
is invertible, then
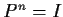
for
some positive integer
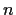
.
Problem 6
Let
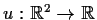
be the function defined by
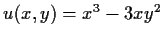
. Show that
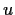
is harmonic and find
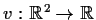
such that the function
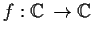
defined by
is analytic.
Problem 7
Evaluate
where
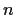
is a positive integer.
Problem 8
Find all solutions of the differential equation
subject to the condition
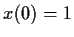
and
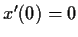
.
Problem 9
Let
![% latex2html id marker 895
$f:[0,1] \to \mbox{$\mathbb{R}^{}$}$](img40-1.gif)
be continuously differentiable, with
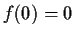
.
Prove that
Problem 10
Let
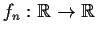
be differentiable for each
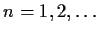
with
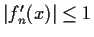
for all n and x. Assume
for all x. Prove that
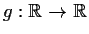
is continuous.
Problem 11
Show that the differential equation
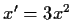
has no solution such
that
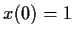
and
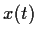
is defined for all real numbers t.
Problem 12
Let
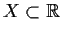
be a nonempty connected set of real numbers. If
every element of
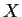
is rational, prove
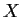
has only one element.
Problem 13
Consider the following four types of transformations:
Here,
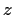
is a variable complex number and the other letters denote
constant complex numbers. Show that each transformation takes
circles to either circles or straight lines.
Problem 14
If
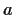
and
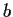
are complex numbers and
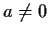
, the set
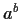
consists of those complex numbers
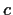
having a logarithm of the form
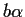
, for some logarithm
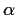
of
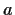
. (That is,
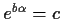
and
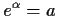
for some complex number
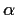
.)
Describe set
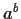
when
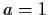
and
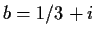
.
Problem 15
Let
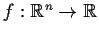
have continuous partial derivatives and satisfy
for all
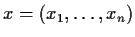
,
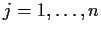
. Prove that
(where
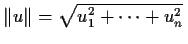
).
Problem 16
Let
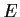
and
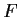
be vector spaces (not assumed to be finite-dimensional).
Let
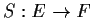
be a linear transformation.
- Prove
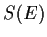 is a vector space.
is a vector space.
- Show
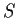 has a kernel
has a kernel 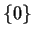 if and only if
if and only if 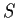 is injective (i.e.,
one-to-one).
is injective (i.e.,
one-to-one).
- Assume
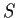 is injective; prove
is injective; prove
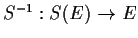 is linear.
is linear.
Problem 17
Let
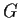
be the set of 3
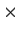
3 real matrices with zeros below
the diagonal and ones on the diagonal.
- Prove
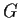 is a group under matrix multiplication.
is a group under matrix multiplication.
- Determine the center of
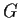 .
.
Problem 18
Suppose the complex number
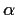
is a root of a polynomial of
degree
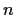
with rational coefficients. Prove that
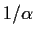
is
also a root of a polynomial of degree
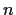
with rational coefficients.
Problem 19
Let
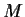
be a real 3
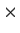
3 matrix such that
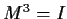
,
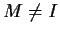
.
- What are the eigenvalues of
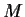 ?
?
- Give an example of such a matrix.
Problem 20
Let
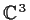
denote the set of ordered triples of complex numbers.
Define a map
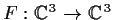
by
Prove that
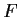
is onto but not one-to-one.



Previous: Summer77
Next: Spring78
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10