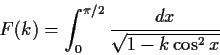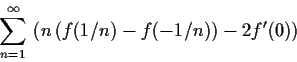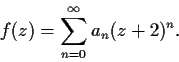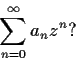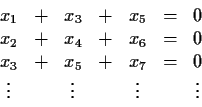Previous: Spring77
Next: Fall77
Preliminary Exam - Summer 1977
Problem 2
Let f be continuous on
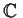
and analytic on
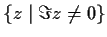
. Prove that
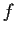
must be analytic on
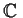
.
Problem 3
Prove that
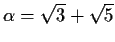
is algebraic over
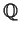
,
by explicitly finding a polynomial with coefficients in
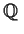
of
which
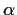
is a root.
Problem 4
Let
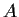
be an
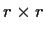
matrix of real numbers. Prove that the infinite sum
of matrices converges (i.e., for each
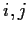
, the sum of
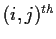
entries converges), and hence that
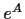
is a well-defined matrix.
Problem 5
Write all values of
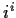
in the form
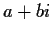
.
Problem 6
Show that
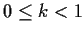
, is an increasing function of
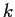
.
Problem 7
Let
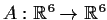
be a linear transformation such that
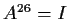
. Show that
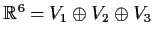
,
where
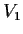
,
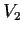
, and
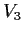
are two-dimensional invariant subspaces for
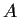
.
Problem 8
Prove that the initial value problem
has a solution
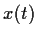
defined for all
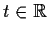
.
Problem 9
Show that every rotation of
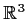
has an
axis; that is, given a
3
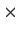
3 real matrix
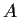
such that
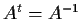
and
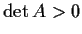
,
prove that there is a nonzero vector v such that Av = v. _matrix,>axis
Problem 10
Suppose that
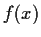
is defined on
![$[-1,1]$](img47-5.gif)
, and that
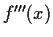
is
continuous. Show that the series
converges.
Problem 11
Let
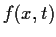
be a
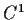
function such that
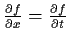
. Suppose that
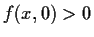
for all
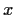
.
Prove that
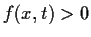
for all
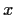
and
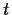
.
Problem 12
Let
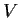
be the vector space of all polynomials of degree
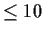
, and
let
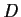
be the differentiation operator on
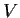
(i.e.,
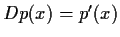
).
- Show that
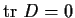 .
.
- Find all eigenvectors of
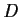 and
and 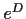 .
.
Problem 13
Let
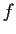
be an analytic function such that
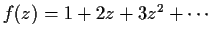
for
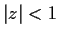
. Define a sequence of real numbers
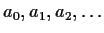
by
What is the radius of convergence of the series
Problem 15
Let
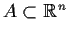
be compact,
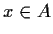
; let
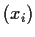
be a
sequence in
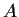
such that every convergent subsequence of
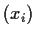
converges to
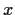
.
- Prove that the entire sequence
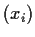 converges.
converges.
- Give an example to show that if
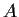 is not compact, the
result in Part 1 is not necessarily true.
is not compact, the
result in Part 1 is not necessarily true.
Problem 16
Use the Residue Theorem to evaluate the integral
where
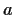
is real and
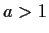
. Explain why the formula obtained for
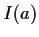
is also valid for certain complex (nonreal) values of
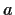
.
Problem 17
In the ring
![% latex2html id marker 1094
$\mbox{$\mathbb{Z}^{}$}[x]$](img88-4.gif)
of polynomials in one variable over the integers,
show that the ideal
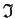
generated by
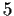
and
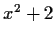
is a maximal ideal.
Problem 18
Let
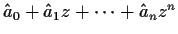
be a polynomial having
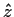
as a simple root. Show that there is a continuous function
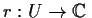
, where
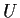
is a neighborhood of
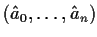
in
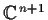
, such that
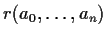
is always a root of
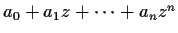
, and
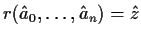
.
Problem 19
Let p be an odd prime. If the congruence
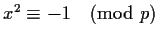
has
a solution, show that
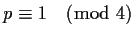
.
Problem 20
Determine all solutions to the following infinite system of linear
equations in the infinitely many unknowns
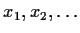
:
How many free parameters are required?



Previous: Spring77
Next: Fall77
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
![% latex2html id marker 685
$\mbox{\bf {F}}[x]$](img3-5.gif) is a vector space over
is a vector space over
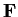 .
.
![% latex2html id marker 689
$\mbox{\bf {F}}_n[x]$](img5-5.gif) of polynomials of degree
of polynomials of degree 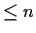 is a
subspace of dimension
is a
subspace of dimension 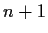 in
in
![% latex2html id marker 695
$\mbox{\bf {F}}[x]$](img8-5.gif) .
.
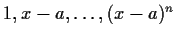 form a basis
of
form a basis
of
![% latex2html id marker 699
$\mbox{\bf {F}}_n[x]$](img10-5.gif) for any
for any
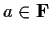 .
.