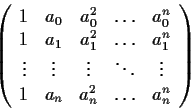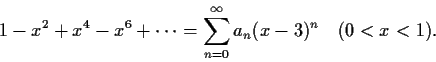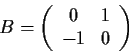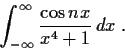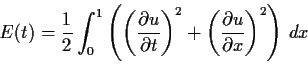Previous: Contents
Next: Summer77
Preliminary Exam - Spring 1977
Problem 1
Suppose
is a differentiable function from the reals into the reals.
Suppose
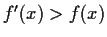
for all
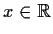
, and
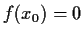
. Prove
that
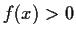
for all

.
Problem 2
Suppose that

is a real valued function of one real variable such
that
exists for all
![$c \in [a,b]$](img9.gif)
. Show that
is Riemann integrable
on
![$[a,b]$](img11.gif)
.
Problem 3
- Evaluate
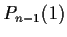 , where
, where 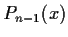 is the polynomial
is the polynomial
- Consider a circle of radius
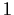 , and let
, and let
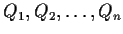 be the vertices of a regular
be the vertices of a regular 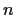 -gon inscribed in the circle. Join
-gon inscribed in the circle. Join
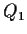 to
to
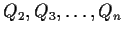 by segments of a straight line. You
obtain
by segments of a straight line. You
obtain 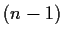 segments of lengths
segments of lengths
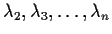 .
Show that
.
Show that
file=../Fig/Pr/Sp77-3,width=2.7in
Problem 4
Prove the Fundamental Theorem of Algebra: Every nonconstant polynomial
with complex coefficients has a complex root.
_Fundamental Theorem>of Algebra
Problem 5
Let
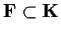
be fields, and
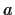
and
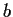
elements of
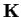
which are algebraic over
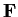
. Show that
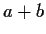
is algebraic over
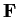
.
Problem 7
A matrix of the form
where the
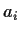
are complex numbers, is called a Vandermonde matrix.
- Prove that the Vandermonde matrix is invertible if
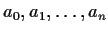 are all different.
are all different.
- If
 are all different, and
are all different, and
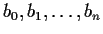 are complex numbers, prove that there is a
unique polynomial
are complex numbers, prove that there is a
unique polynomial  of degree
of degree  with complex coefficients such
that
with complex coefficients such
that 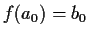 ,
,  ,...,
,...,  .
.
Problem 8
Find a list of real matrices, as long as possible, such that
- the characteristic polynomial of each matrix is
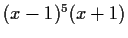 ,
,
- the minimal polynomial of each matrix is
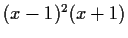 ,
,
- no two matrices in the list are similar to each other.
Problem 9
Find the solution of the differential equation
subject to the conditions
Problem 10
In
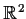
, consider the region
defined by
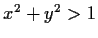
. Find
differentiable real valued functions
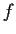
and

on
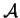
such that
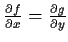
but there is no real valued function
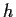
on
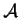
such that
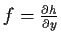
and
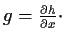
Problem 11
Let the sequence
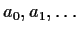
be defined by the equation
Find
Problem 12
Let
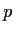
be an odd prime. Let
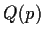
be the set of integers
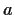
,

, for which the congruence
has a solution. Show that
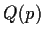
has cardinality
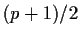
.
Problem 13
Consider the family of square matrices
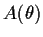
defined by the
solution of the matrix differential equation _matrix,>orthogonal
with the initial condition
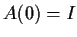
, where
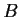
is a constant square matrix.
- Find a property of
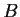 which is necessary and sufficient for
which is necessary and sufficient for
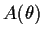 to be orthogonal for all
to be orthogonal for all  ; that is,
; that is,
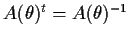 , where
, where 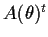 denotes the
transpose of
denotes the
transpose of 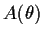 .
.
- Find the matrices
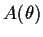 corresponding to
corresponding to
and give a geometric interpretation.
Problem 15
Let
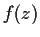
be a nonconstant meromorphic function. A complex number
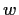
is called
a period of
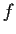
if
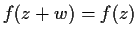
for all
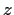
.
- Show that if
 and
and 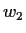 are periods, so are
are periods, so are 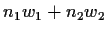 for all integers
for all integers 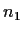 and
and  .
.
- Show that there are, at most, a finite number of periods of
 in any bounded region of the complex plane.
in any bounded region of the complex plane.
Problem 17
Let
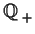
be the multiplicative group of positive rational numbers.
- Is
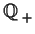 torsion free?
torsion free?
- Is
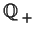 free?
free?
Problem 18
- In
![% latex2html id marker 1152
$\mbox{$\mathbb{R}^{}$}[x]$](img122.gif) , consider the set of polynomials
, consider the set of polynomials 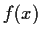 for which
for which
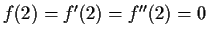 . Prove that this set forms an ideal
and find its monic generator.
. Prove that this set forms an ideal
and find its monic generator.
- Do the polynomials such that
 and
and 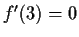 form
an ideal?
form
an ideal?
Problem 19
Suppose that

is a continuous function of the real variables
x and t with continuous second partial derivatives. Suppose that
u and its first partial derivatives are periodic in
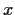
with period
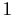
,
and that
Prove that
is a constant independent of
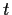
.
Problem 20
Let
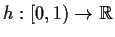
be a function defined on the half-open interval
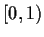
. Prove that if
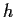
is
uniformly continuous, there exists a unique continuous function
![% latex2html id marker 1210
$g:[0,1]\to\mbox{$\mathbb{R}^{}$}$](img136.gif)
such that
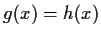
for all
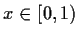
.



Previous: Contents
Next: Summer77
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10