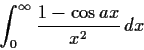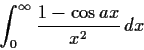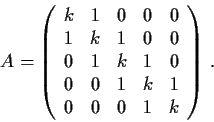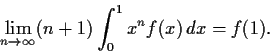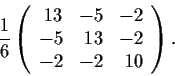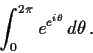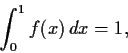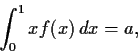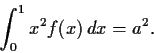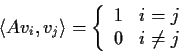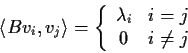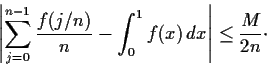Previous: Summer85
Next: Spring86
Preliminary Exam - Fall 1985
Problem 1
Evaluate the integral
for
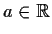
.
Problem 2
Prove that for every
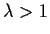
, the equation
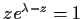
has exactly one root in the disc
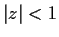
and that this root is real.
Problem 4
Let
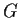
be a finite subgroup of the group
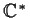
of nonzero complex
numbers under multiplication. Prove that
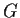
is cyclic.
Problem 5
How many roots does the polynomial
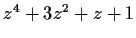
have in the right half
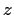
-plane?
Problem 6
Let
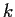
be real,
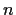
an integer
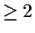
, and let
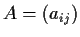
be the
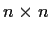
matrix such that all diagonal entries
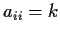
,
all entries
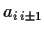
immediately above or below the diagonal
equal
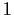
, and all other entries equal
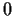
. For example, if
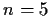
,
Let
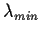
and
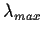
denote the smallest and
largest eigenvalues of
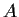
, respectively. Show that
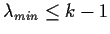
and
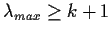
.
Problem 7
Let
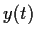
be a real valued solution, defined for
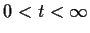
, of
the differential equation
Show that
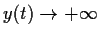
as
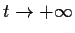
.
Problem 8
Let
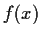
,
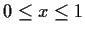
, be a real valued continuous function.
Show that
Problem 9
Let
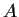
be the symmetric matrix
We denote by
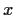
the column vector
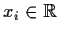
, and by
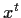
its transpose
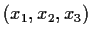
.
Let
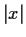
denote the length of the vector
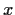
. As
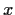
ranges
over the set of vectors for which
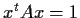
, show that
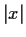
is bounded, and determine its least upper bound.
Problem 10
Let
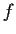
and
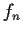
,
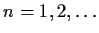
, be functions from
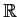
to
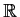
.
Assume that
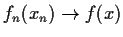
as
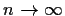
whenever
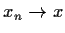
. Show that
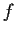
is continuous. Note: The functions
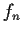
are not assumed to be continuous.
Problem 11
Let
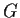
be a subgroup of the symmetric group on six letters,
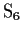
. Assume that
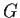
has an element of order
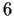
. Prove that
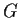
has a normal subgroup
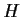
of index
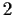
.
Problem 13
Let
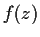
be analytic on the right half-plane
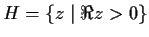
and suppose
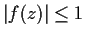
for
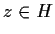
. Suppose also that
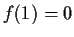
.
What is the largest possible value of
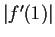
?
Problem 15
Let
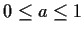
be given. Determine all nonnegative
continuous functions
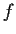
on
![$[0,1]$](img85-25.gif)
which satisfy the following
three conditions:
Problem 16
Let
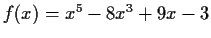
and
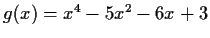
.
Prove that there is
an integer
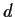
such that the polynomials
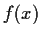
and
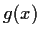
have
a common root in the field
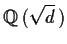
. What is
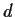
?
Problem 17
Let
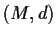
be a nonempty complete metric space. Let
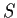
map
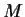
into
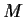
,
and write
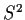
for
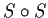
; that is,
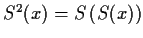
.
Suppose that
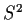
is a
strict contraction; that is, there is a constant
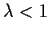
such that for all points
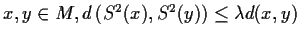
. Show that
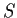
has
a unique fixed point in
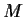
. _map>strict contraction
Problem 18
Let
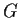
be a group. For any subset
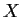
of
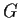
, define its centralizer
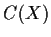
to be
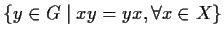
. Prove the
following:
- If
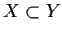 , then
, then
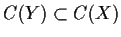 .
.
-
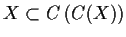 .
.
-
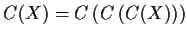 .
.
Problem 19
An n
n real matrix
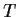
is
positive definite if
_matrix,>positive definite
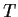
is symmetric and
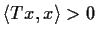
for all nonzero vectors
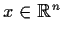
, where
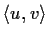
is the standard inner product.
Suppose that
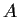
and
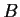
are two positive definite real matrices.
- Show that there is a basis
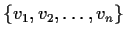 of
of
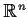 and real numbers
and real numbers
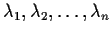 such that,
for
such that,
for
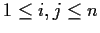 :
:
and
- Deduce from Part 1 that there is an invertible real matrix
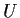 such that
such that 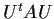 is the identity matrix and
is the identity matrix and 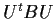 is
diagonal.
is
diagonal.
Problem 20
Let
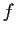
be a differentiable function on
![$[0,1]$](img135-7.gif)
and let
Let
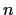
be a positive integer. Prove that



Previous: Summer85
Next: Spring86
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10