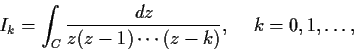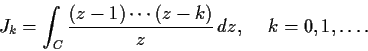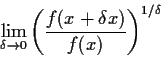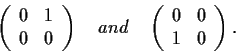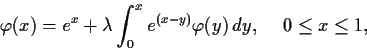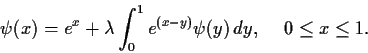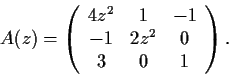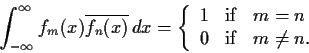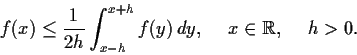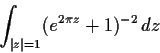Previous: Fall85
Next: Fall86
Preliminary Exam - Spring 1986
Problem 1
Let
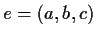
be a unit vector in
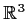
and let
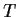
be the
linear transformation on
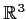
of rotation by
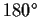
about
e. Find the matrix for
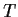
with respect to the standard basis.
Problem 2
Let f be a continuous real valued function on
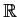
such that
for all x. Prove that f is constant.
Problem 3
Let
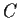
be a simple closed contour enclosing the points
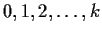
in the complex plane, with positive
orientation. Evaluate the integrals
Problem 4
Let
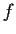
be a positive differentiable function on
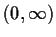
.
Prove that
exists (finitely) and is nonzero for each x.
Problem 5
Prove that there exists only one automorphism of the field of
real numbers; namely the identity automorphism.
Problem 7
For
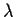
a real number, find all solutions of the integral
equations
Problem 8
Let the 3
3 matrix function

be defined on the complex
plane by
How many distinct values of
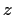
are there such that
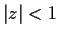
and
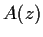
is not invertible?
Problem 9
Let
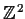
be the group of lattice points in the plane (ordered pairs
of integers, with coordinatewise addition as the group operation).
Let
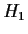
be the subgroup generated by the two elements
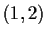
and
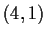
, and
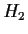
the subgroup generated by the two elements
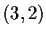
and
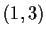
. Are the quotient groups
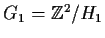
and
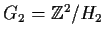
isomorphic?
Problem 10
Suppose addition and multiplication are defined on
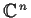
, complex
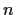
-space, coordinatewise, making
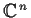
into a ring. Find all
ring homomorphisms of
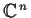
onto
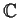
.
Problem 11
Let the complex valued functions
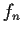
,
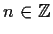
, be defined
on
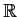
by _function,>orthonormal
Prove that these functions are
orthonormal; that is,
Problem 12
Let
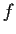
be a real valued continuous function on
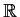
satisfying
the
mean value inequality below:
Prove:
- The maximum of
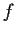 on any closed interval is assumed at one
of the endpoints.
on any closed interval is assumed at one
of the endpoints.
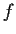 is convex.
is convex.
_function,>convex
Problem 13
Let
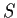
be a nonempty commuting set of
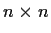
complex matrices
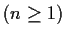
.
Prove that the members of
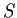
have a common eigenvector.
Problem 14
Let
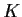
be a compact subset of
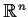
and
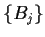
a
sequence of open balls that covers
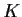
. Prove that there is a positive
number
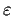
such that each
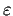
-ball centered at a point
of
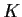
is contained in one of the balls
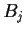
.
Problem 15
Consider
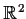
be equipped with the Euclidean metric
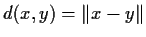
. Let
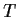
be an isometry of
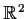
into itself.
Prove that
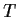
can be represented as
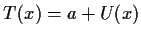
, where a is
a vector in
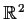
and
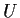
is an orthogonal linear transformation.
Problem 16
Let
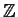
be the ring of integers,
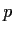
a prime, and
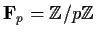
the field of
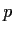
elements.
Let
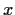
be an indeterminate, and set
![% latex2html id marker 1115
$R_1=\mbox{\bf {F}}_p[x]/\langle x^2-2 \rangle$](img94-25.gif)
,
![% latex2html id marker 1117
$R_2 = \mbox{\bf {F}}_p[x]/\langle x^2-3\rangle $](img95-25.gif)
.
Determine whether the rings
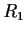
and
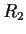
are isomorphic in each of the cases
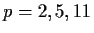
.
Problem 17
Let
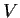
be a finite-dimensional vector space (over
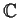
) of
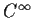
complex valued functions on
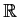
(the linear operations being defined
pointwise). Prove that if
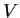
is closed under differentiation (i.e.,
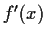
belongs to
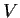
whenever
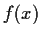
does), then
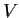
is
closed under translations (i.e.,
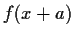
belongs to
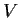
whenever
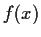
does, for all real numbers
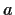
).
Problem 18
Let
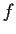
,
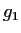
,
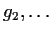
be entire functions. Assume that
-
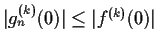 for all
for all 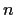 and
and 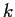 ;
;
-
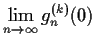 exists for all
exists for all 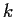 .
.
Prove that the sequence
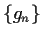
converges uniformly
on compact sets and that its limit is an entire function.
Problem 19
Prove that the additive group of
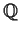
, the rational number field,
is not finitely generated.
Note: See also Problems ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) and
and ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 20
Evaluate
where the integral is taken in counterclockwise direction.



Previous: Fall85
Next: Fall86
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10