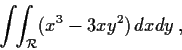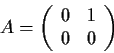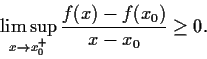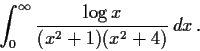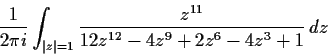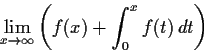Previous: Spring86
Next: Spring87
Preliminary Exam - Fall 1986
Problem 1
The Arzelà-Ascoli Theorem asserts that the sequence
of continuous real valued functions on
a metric space

is precompact (i.e., has a uniformly convergent
subsequence) if
- (i)
 is compact,
is compact,
- (ii)
-
 (where
(where
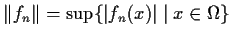 ),
),
- (iii)
- the sequence is equicontinuous.
Give examples of sequences which are not precompact such that:
(i) and (ii) hold but (iii) fails; (i) and (iii) hold but (ii) fails;
(ii) and (iii) hold but (i) fails. Take
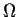
to be a subset
of the real line. Sketch the graph of a typical member of the
sequence in each case.
Problem 2
Let the points

,
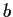
, and
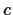
lie on the unit circle of the complex
plane and satisfy
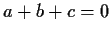
. Prove that
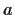
,
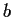
, and
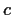
form the
vertices of an equilateral triangle.
Problem 4
Show that the polynomial
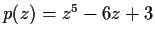
has five distinct complex
roots, of which exactly three (and not five) are real.
Problem 5
Let
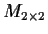
denote the vector space of complex 2
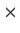
2 matrices.
Let
and let the linear transformation
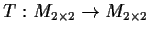
be
defined by

. Find the Jordan Canonical Form for
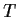
.
Problem 6
Prove the following theorem, or find a counterexample: If
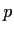
and
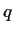
are continuous real valued functions on
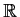
such that
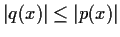
for all
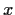
, and if every solution
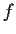
of the differential
equation
satisfies
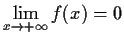
, then every solution
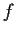
of the differential equation
satisfies
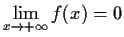
.
Problem 7
Let
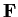
be a field containing
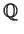
such that
![% latex2html id marker 815
$[\mbox{\bf {F}}:\mbox{$\mathbb{Q}\,^{}$}] = 2$](img36-30.gif)
.
Prove that there exists a unique integer
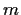
such that
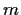
has no multiple
prime factors and
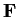
is isomorphic to
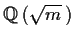
.
Problem 8
Let
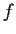
be a continuous real valued function on
![$[0,1]$](img42-30.gif)
such that,
for each
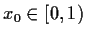
,
Prove that
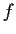
is nondecreasing.
Problem 10
For

a real valued function on the real line, define the function

by
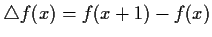
. For
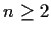
,
define
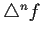
recursively by
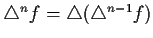
. Prove that
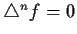
if
and only if
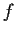
has the form

where
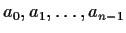
are periodic functions of period
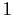
.
Problem 11
Let
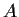
be an
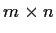
matrix with entries in a field
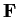
. Define
the row rank and the column rank of
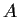
and show from first principles
that they are equal.
Problem 12
Let
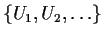
be a cover of

by open sets. Prove
that there is a cover
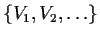
such that
-
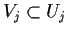 for each
for each 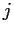 ;
;
- each compact subset of
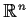 is disjoint from all but
finitely many of the
is disjoint from all but
finitely many of the 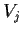 .
.
Problem 13
Let
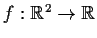
be defined by:
Determine all points at which
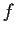
is differentiable.
Problem 14
Let
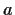
and
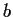
be real numbers. Prove that there are two
orthogonal unit vectors
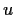
and
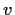
in

such that
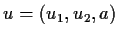
and

if and only if
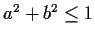
.
Problem 15
Prove that if
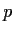
is a prime number

then the polynomial
is irreducible in
![% latex2html id marker 1021
$\mathbb{Q}[x]$](img83-29.gif)
.
Problem 16
Discuss the solvability of the differential equation
with the initial condition
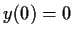
. Does a solution exist
in some interval about
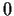
? If so, is it unique?
Problem 17
Let
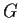
be a subgroup of
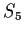
, the group of all permutations on the
set

. Prove that if
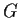
contains a
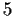
-cycle and a

-cycle, then

.
Problem 18
Evaluate
where the direction of integration is counterclockwise.
Problem 19
Prove that if six people are riding together in an Evans Hall
elevator, there is either a three-person subset of mutual friends
(each knows the other two) or a three-person subset of mutual
strangers (each knows neither of the other two).
Problem 20
Let
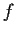
be a real valued continuous function on
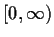
such
that
exists. Prove that



Previous: Spring86
Next: Spring87
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
 is compact,
is compact,
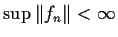 (where
(where
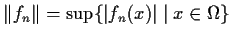 ),
),