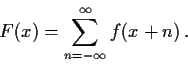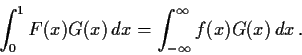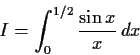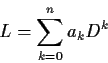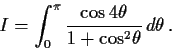Previous: Fall86
Next: Fall87
Preliminary Exam - Spring 1987
Problem 1
A standard theorem states that a continuous real valued function
on a compact set is bounded. Prove the converse: If
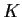
is a subset
of
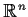
and if every continuous real valued function on

is bounded, then
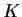
is compact.
Problem 2
Let the transformation
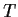
from the subset

of
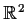
into
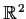
be defined by
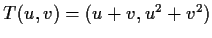
.
- Prove that
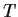 is locally one-to-one.
is locally one-to-one.
- Determine the range of
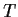 , and show that
, and show that 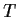 is globally one-to-one.
is globally one-to-one.
Problem 3
Let

be a complex valued function in the open unit disc,
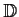
,
of the complex plane such that the functions
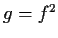
and
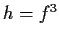
are both analytic. Prove that
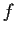
is analytic in
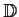
.
Problem 4
Let
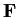
be a finite field with
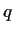
elements and let
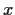
be an
indeterminate. For
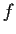
a polynomial in
![% latex2html id marker 763
$\mbox{\bf {F}}[x]$](img23-31.gif)
, let
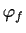
denote
the corresponding function of
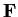
into
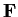
, defined by
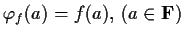
. Prove that if

is
any function of
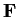
into
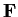
, then there is an
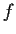
in
![% latex2html id marker 781
$\mbox{\bf {F}}[x]$](img32-31.gif)
such that
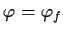
. Prove that
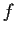
is uniquely determined by
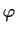
to within addition of a multiple of
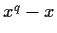
.
Problem 5
Let
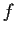
be a continuous real valued function on

satisfying
where
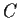
is a positive constant.
Define the function
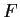
on
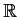
by
- Prove that
 is continuous and periodic with period
is continuous and periodic with period 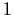 .
.
- Prove that if
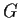 is continuous and periodic with period
is continuous and periodic with period 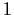 , then
, then
Problem 6
Let
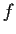
be an analytic function in the open unit disc of the
complex plane such that
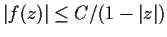
for all
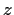
in the disc, where

is a positive constant. Prove
that
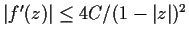
.
Problem 7
Let p, q and r be continuous real valued functions on
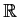
, with
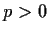
. Prove that the differential equation
is equivalent to (i.e., has exactly the same solutions as) a
differential equation of the
form
where a is continuously differentiable and b is continuous.
Problem 8
Prove that if the nonconstant polynomial
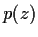
, with complex
coefficients, has all of its roots in the half-plane

,
then all of the roots of its derivative are in the same half-plane.
Problem 9
Let
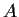
be an
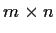
matrix with rational entries and

an
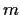
-dimensional column vector with rational entries. Prove or
disprove: If the equation
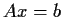
has a solution
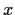
in
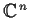
,
then it has a solution with
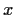
in
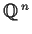
.
Problem 10
Prove that any finite group of order
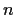
is isomorphic to a
subgroup of

, the group of
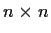
orthogonal real
matrices.
Problem 11
Show that the equation
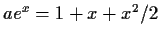
, where
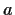
is
a positive constant, has exactly one real root.
Problem 12
Evaluate the integral
to an accuracy of two decimal places; that is, find a number
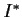
such that
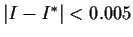
.
Problem 13
Let

be a real valued
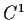
function defined in the punctured
plane
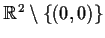
. Assume that the partial derivatives
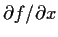
and
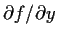
are
uniformly bounded; that is, there exists a positive constant
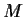
such that
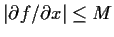
and
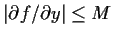
for all points
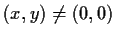
. Prove that
exists. _function,>uniformly bounded
Problem 15
Prove or disprove: If the function
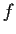
is analytic in the
entire complex plane, and if
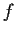
maps every unbounded sequence to
an unbounded sequence, then
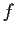
is a polynomial.
Problem 16
Let
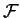
be a uniformly bounded, equicontinuous family of real valued
functions on the metric space
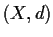
. Prove that the function
is continuous.
Problem 17
Let
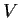
be a finite-dimensional linear subspace of

(the space of complex valued, infinitely differentiable functions).
Assume that
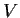
is closed under
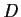
, the operator of differentiation
(i.e.,
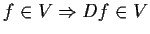
). Prove that there is
a constant coefficient differential operator
such that
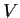
consists of all solutions of the differential equation
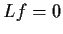
.
Problem 18
Let

and
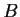
be two diagonalizable
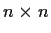
complex matrices
such that

. Prove that there is a basis for
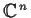
that
simultaneously diagonalizes
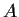
and
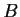
.
Problem 19
Let
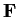
be a field. Prove that every finite subgroup of the
multiplicative group of nonzero elements of
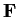
is cyclic.



Previous: Fall86
Next: Fall87
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10