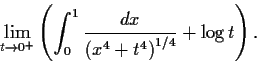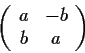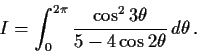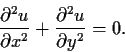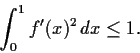Previous: Spring87
Next: Spring88
Preliminary Exam - Fall 1987
Problem 1
Prove that
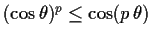
for

and
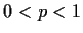
.
Problem 2
Suppose that
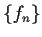
is a sequence of
nondecreasing functions which map the unit interval into
itself. Suppose that
pointwise and that
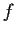
is a continuous function. Prove
that
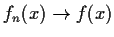
uniformly as
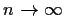
,
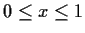
. Note that the functions

are not
necessarily continuous.
Problem 3
Show that the following limit exists
and is finite:
Problem 4
Let u and v be two real valued
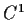
functions on
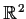
such that
the gradient
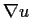
is never
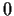
, and such that, at each point,
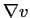
and

are linearly dependent vectors. Given
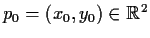
, show that there is a
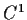
function
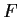
of one variable such that
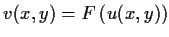
in
some neighborhood of
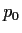
.
Problem 5
Calculate
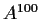
and

, where
Problem 6
Let
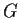
and

be finite groups of relatively prime order. Show that
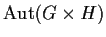
, the group of automorphisms of
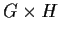
, is
isomorphic to the direct product of
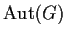
and
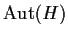
.
Problem 7
Let
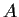
and
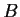
be real n
n symmetric matrices with
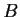
positive
definite. Consider the function defined for
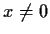
by
- Show that
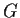 attains its maximum value.
attains its maximum value.
- Show that any maximum point
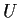 for
for  is an eigenvector
for a certain matrix related to
is an eigenvector
for a certain matrix related to 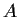 and
and  and show which matrix.
and show which matrix.
Problem 8
Let
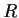
be the set of 2
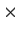
2 matrices of the form
where a, b are elements of a given field

. Show that with
the usual matrix operations,
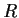
is a commutative ring
with identity. For which of the following fields
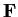
is
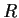
a field:
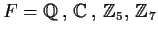
?
Problem 9
Evaluate the integral
Problem 10
If

is analytic in the open disc
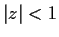
, and
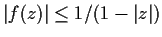
, show that
Problem 11
Let
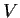
be a finite-dimensional vector space and
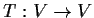
a diagonalizable linear transformation.
Let
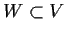
be a
linear subspace which is mapped into itself by
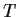
. Show that the
restriction of
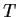
to
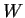
is diagonalizable.
Problem 12
Given two
real 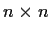
matrices
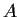
and
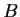
, suppose that there is
a nonsingular
complex matrix
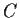
such that
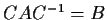
.
Show
that there exists a
real nonsingular
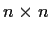
matrix
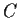
with
this property.
Problem 13
Let
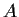
be the group of rational numbers under addition, and let
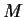
be the group of positive rational numbers under multiplication.
Determine all homomorphisms
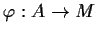
.
Problem 14
Show that
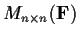
, the ring of all
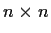
matrices over the
field
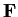
, has no proper two sided ideals.
Problem 15
Let
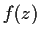
be analytic for
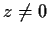
, and suppose that
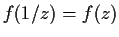
.
Suppose also that
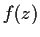
is real for all
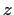
on the unit
circle
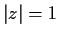
. Prove that
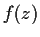
is real for all real
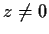
.
Problem 16
How many zeros (counting multiplicities) does the polynomial
have in the annular region
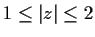
?
Problem 17
Let
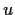
be a positive
harmonic function on
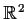
; that is,
Show that
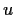
is constant. _function,>harmonic
Problem 18
Find a curve
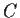
in
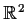
, passing through the point
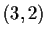
,
with the following property: Let
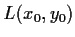
be the segment of
the tangent line to

at

which lies in the first
quadrant. Then each point
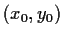
of
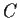
is the midpoint of

.
file=../Fig/Pr/Fa87-18,width=2.7in
Problem 19
Define a sequence of positive numbers as follows. Let
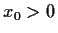
be
any positive number, and let

. Prove that
this sequence converges, and find its limit.
Problem 20
Let
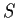
be the set of all real
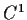
functions
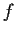
on
![$[0,1]$](img103-22.gif)
such
that
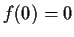
and
Define
Show that the function
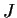
is bounded on
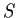
, and compute its
supremum. Is there a function
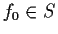
at which
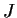
attains
its maximum value? If so, what is
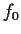
?



Previous: Spring87
Next: Spring88
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10