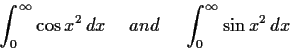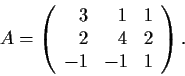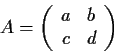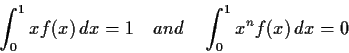Previous: Fall87
Next: Fall88
Preliminary Exam - Spring 1988
Problem 1
Suppose that
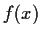
,
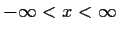
, is a continuous
real valued function, that
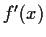
exists for
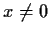
, and that
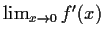
exists. Prove that
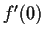
exists.
Problem 2
Determine the last digit of
in the decimal system.
Problem 3
If a finite homogeneous system of linear equations with rational
coefficients has a nontrivial complex solution, need it have a
nontrivial rational solution? Give a proof or a counterexample.
Problem 4
True or false: A function
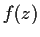
analytic on
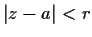
and
continuous on
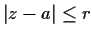
extends, for some
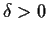
, to
a function analytic on
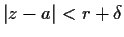
? Give a proof
or a counterexample.
Problem 5
Let
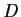
be a group of order
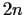
, where
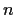
is odd, with a subgroup
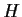
of
order
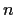
satisfying

for all h in
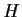
and all
x in
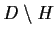
. Prove that
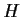
is commutative and that every
element of
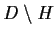
is of order
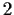
.
Problem 6
Prove or disprove: There is a real
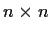
matrix
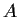
such that
if and only if
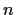
is even.
Problem 7
Let
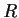
be a commutative ring with unit element and
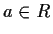
. Let
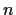
and
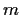
be positive integers, and write
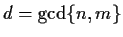
. Prove that
the ideal of
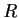
generated by
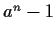
and

is the same as the
ideal generated by
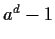
.
Problem 8
For
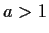
and
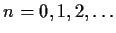
, evaluate the integrals
Problem 9
Prove that the integrals
converge.
Problem 11
Let
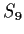
denote the group of permutations of
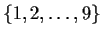
and let
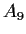
be the subgroup consisting of all even permutations. Denote by
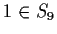
the identity permutation. Determine the minimum of all
positive integers
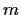
such that every
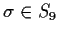
satisfies
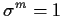
. Determine also the minimum of all positive integers

such that every
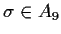
satisfies
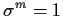
.
Problem 12
For each real value of the parameter
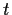
,
determine the number of real roots, counting multiplicities, of
the cubic polynomial
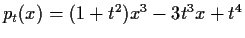
.
Problem 13
Find all groups
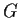
such that every automorphism of
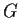
is trivial.
Problem 14
Let the function f be analytic in the open unit disc of the
complex plane and real valued on the radii
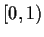
and
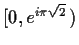
. Prove that f is constant.
Problem 15
Compute
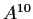
for the matrix
Problem 16
Let

be a set and
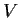
a real vector space of real valued functions
on
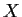
of dimension
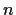
,
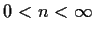
. Prove that there are
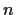
points
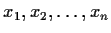
in
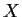
such that the map

of
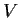
to

is an
isomorphism (i.e., one-to-one and onto). (The operations of
addition and scalar multiplication in
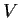
are assumed to be the
natural ones.)
Problem 18
For which positive integers
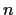
is there a 2
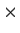
2
matrix
with integer entries and order
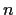
; that is,
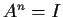
but

for
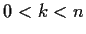
? _matrix,>order n
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 19
Show that you can represent the set of nonnegative integers,
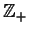
,
as the union of two disjoint subsets
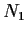
and

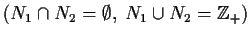
such that
neither
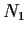
nor
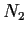
contains an infinite arithmetic progression.
Problem 20
Does there exist a continuous real valued function
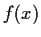
,
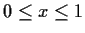
, such that
for

? Give an example or a proof that no
such
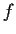
exists.



Previous: Fall87
Next: Fall88
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10