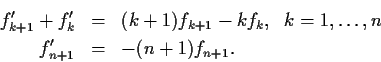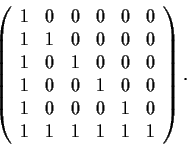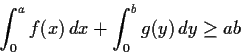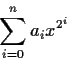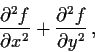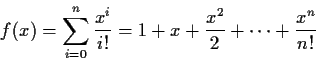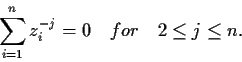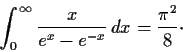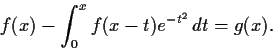Previous: Spring88
Next: Spring89
Preliminary Exam - Fall 1988
Problem 1
Let
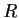
be a finite ring. Prove that there are positive integers m and
n with
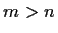
such that
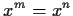
for every
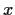
in
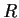
.
Problem 2
Determine the group
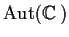
of all one-to-one analytic maps of
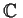
onto
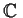
.
Problem 3
Let the real valued functions
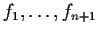
on
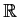
satisfy
the system of differential equations
Prove that for each
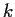
,
Problem 4
Find the Jordan Canonical Form of the matrix
Problem 5
Let
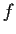
be a continuous, strictly increasing function from
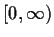
onto
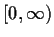
and let
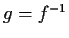
.
Prove that
for all positive numbers
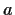
and
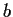
, and determine the condition
for equality.
Problem 6
Let
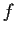
be a function from
![$[0,1]$](img23-34.gif)
into itself whose graph
is a closed subset of the unit square. Prove that
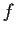
is continuous.
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 7
Find all abelian groups of order
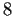
, up to isomorphism. Then identify
which type occurs in each of
-
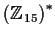 ,
,
-
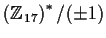 ,
,
- the roots of
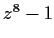 in
in
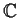 ,
,
-
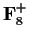 ,
,
-
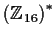 .
.
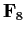
is the field of eight elements, and
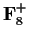
is
its underlying additive group;
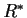
is the group of invertible
elements in the ring
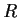
, under multiplication.
Problem 8
Do the functions
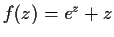
and
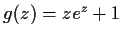
have the same
number of zeros in the strip
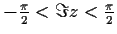
?
Problem 9
Let
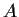
and
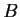
be real symmetric n
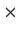
n matrices. Assume that
the eigenvalues of
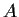
all lie in the interval
![$[a_1,a_2]$](img44-34.gif)
and those
of
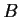
all lie in the interval
![$[b_1,b_2]$](img46-34.gif)
. Prove that the eigenvalues
of
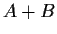
all lie in the interval
![$[a_1+b_1, a_2+b_2]$](img48-34.gif)
.
Problem 10
Find (up to isomorphism) all groups of order
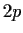
, where
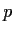
is a
prime (
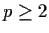
).
Problem 11
Let
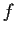
be an analytic function on a disc
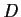
whose center is the
point
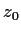
. Assume that
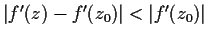
on
D. Prove that
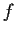
is one-to-one on
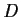
.
Problem 12
Let n be a positive integer and let
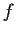
be a polynomial in
![% latex2html id marker 938
$\mbox{$\mathbb{R}^{}$}[x]$](img59-34.gif)
of degree
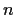
. Prove that there are real numbers
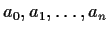
,
not all equal to zero, such that the polynomial
is divisible by f.
Problem 13
Let
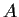
be a complex
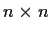
matrix, and let
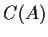
be the
commutant
of
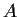
; that is, the set of complex
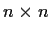
matrices
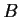
such that
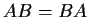
. (It is obviously a subspace of
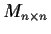
, the vector space of
all complex
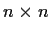
matrices.) Prove that
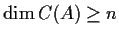
.
_matrix,>commutant of a
Problem 14
Let the group
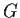
be generated by two elements,
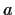
and
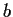
, both of
order
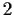
. Prove that
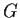
has a subgroup of index
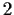
.
Problem 15
Prove that a real valued
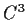
function
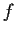
on
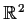
whose Laplacian,
is everywhere positive cannot have a local maximum.
Problem 16
Let
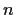
be a positive integer. Prove that the polynomial
in
![% latex2html id marker 1040
$\mbox{$\mathbb{R}^{}$}[x]$](img85-33.gif)
has
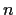
distinct complex zeros,
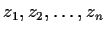
, and that
they satisfy
Problem 18
Let
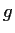
be a continuous real valued function on
![$[0,1]$](img91-32.gif)
. Prove that
there exists a continuous real valued function
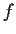
on
![$[0,1]$](img93-32.gif)
satisfying the equation



Previous: Spring88
Next: Spring89
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10