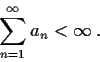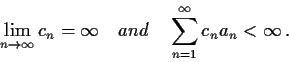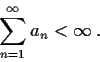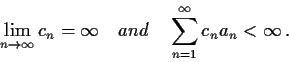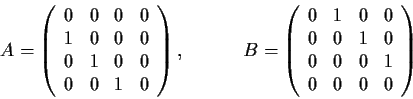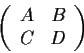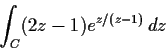Previous: Fall88
Next: Fall89
Preliminary Exam - Spring 1989
Problem 1
Let

be positive numbers such that
Prove that there are positive numbers
such that
Problem 2
Let

be a field,
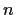
and

positive integers, and
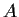
an

matrix with entries in

such that
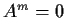
.
Prove that
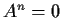
.
Problem 3
Let f be a continuous real valued function on
![$[0,1]\times[0,1]$](img13-32.gif)
.
Let the function g on
![$[0,1]$](img14-32.gif)
be defined by
Prove that g is continuous.
Problem 4
Prove that if
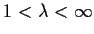
, the function
has only one zero in the half-plane

, and this zero is on the real axis.
Problem 6
Let

be the subspace of
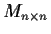
(the vector space of all real
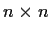
matrices) generated by all matrices of the form
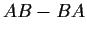
with
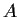
and

in
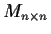
. Prove that
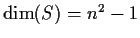
.
Problem 7
Let
Find the general solution of the matrix differential equation
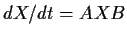
for the unknown
4
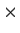
4 matrix function

.
Problem 8
Let
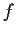
be an analytic function mapping the open unit disc,

,
into itself. Assume that there are two points
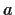
and
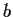
in
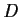
,
with

, such that
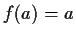
and
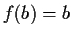
. Prove
that
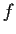
is the identity function (
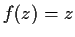
).
Problem 9
For

a group and
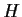
a subgroup, let

denote the collection
of left cosets of
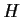
in

. Prove that if
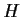
and
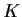
are two subgroups
of
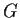
of infinite index, then
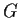
is not a finite union of cosets
from
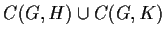
.
Problem 10
Let the real
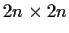
matrix

have the form
where
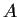
,
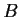
,
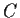
, and
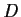
are
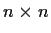
matrices that commute with one
another. Prove that
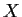
is invertible if and only if
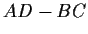
is invertible.
Problem 11
Let
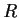
be a ring with at least two elements. Suppose that for each nonzero
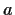
in

there is a unique

in
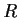
(depending on

) with
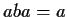
.
Show that
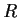
is a division ring.
Problem 12
Evaluate
where
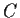
is the circle
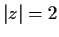
with counterclockwise orientation.
Problem 13
Let

be the dihedral group, the group of rigid motions of a regular
n-gon
. (It is a noncommutative group of order
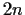
.) Determine
its center
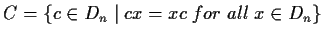
.
Problem 14
Suppose
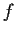
is a continuously differentiable map of
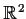
into
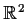
.
Assume that
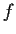
has only finitely many singular points, and that for
each positive number
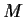
, the set
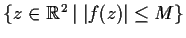
is
bounded. Prove that
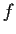
maps
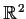
onto
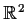
.
Problem 15
Let
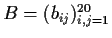
be a real
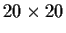
matrix such that
Prove that
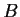
is nonsingular.
Problem 16
Let
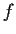
and

be entire functions such that
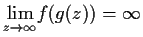
.
Prove that
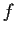
and
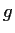
are polynomials.
Problem 18
Let
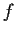
be a real valued function on
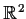
with the following properties:
- For each
 in
in 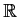 , the function
, the function
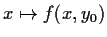 is
continuous.
is
continuous.
- For each
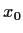 in
in 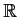 , the function
, the function
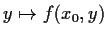 is
continuous.
is
continuous.
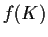 is compact whenever
is compact whenever 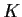 is a compact subset of
is a compact subset of
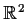 .
.
Prove that
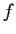
is continuous.



Previous: Fall88
Next: Fall89
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10