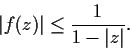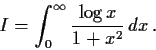Previous: Spring89
Next: Spring90
Preliminary Exam - Fall 1989
Problem 1
Let

be a finite abelian group, and
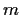
the maximum of the orders of
the elements of

. Put
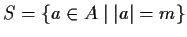
. Prove
that
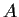
is generated by
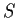
.
Problem 2
Let
![% latex2html id marker 679
$f:[0,1]\to\mbox{$\mathbb{R}^{}$}$](img7-33.gif)
be a real valued continuously differentiable
function with
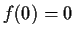
. Suppose also that there is a constant
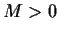
such that, for
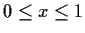
,
Prove that

for
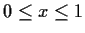
.
Problem 3
Let
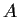
be a real, upper-triangular,
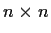
matrix that commutes with
its transpose. Prove that
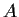
is diagonal.
Problem 4
Let
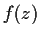
be analytic for
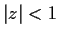
and suppose that
Show that
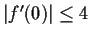
.
Problem 5
Let
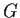
be a group,
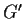
its commutator subgroup, and
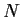
a normal subgroup
of
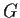
. Suppose that
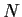
is cyclic. Prove that
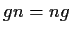
for all
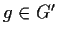
and all
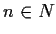
.
Problem 6
Let
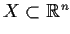
be a closed set and r a fixed positive real number.
Let

.
Show that
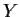
is closed.
Problem 7
Let
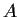
and
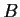
be diagonalizable linear transformations of
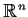
into
itself such that
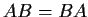
. Let

be an eigenspace of
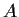
. Prove that
the restriction of
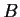
to
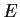
is diagonalizable.
Problem 8
Evaluate the integral
Problem 9
Let
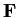
be a field,
![% latex2html id marker 825
$\mbox{\bf {F}}[x]$](img42-33.gif)
the polynomial ring in one variable
over

, and
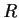
a subring of
![% latex2html id marker 831
$\mbox{\bf {F}}[x]$](img45-33.gif)
with
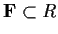
.
Prove that there
exists a finite set
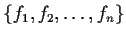
of elements of
![% latex2html id marker 837
$\mbox{\bf {F}}[x]$](img48-33.gif)
such that
![% latex2html id marker 839
$R = \mbox{\bf {F}}[f_1,f_2,\ldots,f_n]$](img49-33.gif)
.
Problem 10
Let
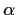
be a number in
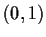
. Prove that any
sequence

of real
numbers satisfying the recurrence relation
has a limit, and find an expression for the limit in
terms of
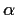
,

and
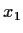
.
Problem 11
Let
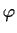
be Euler's totient function; so if
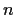
is a positive
_Euler>totient function
integer, then
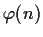
is the number of integers
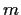
for which
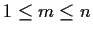
and
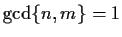
. Let
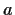
and
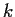
be two integers, with

,
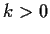
. Prove that
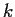
divides
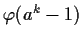
.
Problem 12
Let
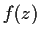
be analytic in the annulus
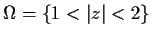
.
Assume that
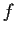
has no zeros in

. Show that there exists an
integer
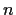
and an analytic function
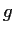
in

such that, for
all
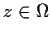
,

.
Problem 13
Let
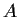
be an

real matrix,
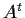
its
transpose. Show that
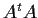
and
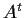
have the same
range. In other words, given
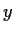
, show that the equation

has a solution
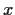
if and only if the equation
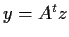
has a solution

.
Problem 14
Let
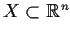
be compact and let
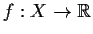
be continuous.
Given
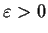
, show there is an
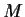
such that for all
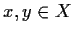
,
Problem 15
Let
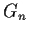
be the free group on
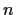
generators. Show that
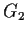
and
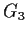
are not isomorphic.
Problem 16
Prove that the polynomial
has at least one root in the disc

.
Problem 17
Let
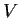
be a vector space of finite-dimension
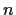
over a field of characteristic
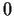
. Prove that
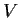
is not the union of finitely many subspaces of dimension

.
Problem 18
Let the function
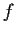
from
![$[0,1]$](img106-24.gif)
to
![$[0,1]$](img107-23.gif)
have the following properties:
Prove that the arclength of the graph of

does not exceed
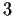
.



Previous: Spring89
Next: Spring90
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10