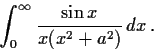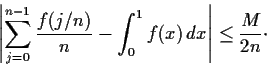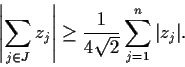Previous: Fall89
Next: Fall90
Preliminary Exam - Spring 1990
Problem 1
Let
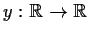
be a
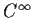
function that satisfies
the differential equation
for
![$x \in [0,L]$](img4-36.gif)
, where
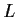
is a positive real number. Suppose
that
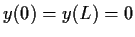
. Prove that
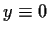
on
![$[0,L]$](img8-36.gif)
.
Problem 2
Let
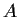
be a complex
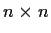
matrix that has
finite order; that is,
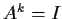
for some positive integer
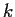
. Prove that
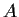
is diagonalizable.
_matrix,>finite order
Problem 3
Let
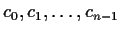
be complex numbers. Prove that all the
zeros of the polynomial
lie in the open disc with center
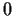
and radius
Problem 4
Let
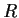
be a commutative ring with
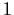
, and
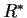
be its group
of units. Suppose that the additive group of
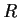
is generated by
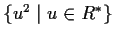
. Prove that
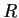
has, at most, one ideal
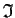
for which
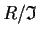
has cardinality
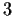
.
Problem 5
Suppose
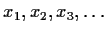
is a sequence of nonnegative real numbers
satisfying
for all
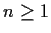
. Prove that
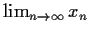
exists.
Problem 6
Give an example of a continuous function
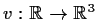
with
the property that
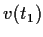
,
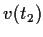
, and
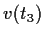
form a basis for
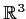
whenever
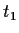
,
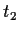
, and
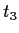
are distinct points of
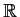
.
Problem 7
Let
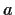
be a positive real number. Evaluate the improper integral
Problem 8
Let
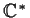
be the multiplicative group of nonzero complex numbers.
Suppose that
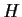
is a subgroup of finite index of
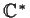
. Prove that

.
Problem 9
Let the real valued function
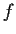
on
![$[0,1]$](img47-36.gif)
have the following two
properties:
Prove that
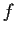
is continuous.
Problem 10
Show that there are at least two nonisomorphic nonabelian groups
of order
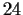
, of order
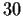
and order
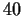
.
Problem 11
Let the function
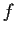
be analytic and bounded in the complex half-plane
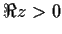
. Prove that for any positive real number
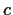
, the
function
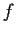
is uniformly continuous in the half-plane
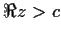
.
Problem 12
Let
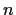
be a positive integer, and let
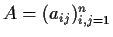
be
the n
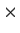
n matrix with
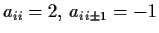
,
and
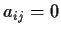
otherwise; that is,
Prove that every eigenvalue of
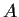
is a positive real number.
Problem 13
Let
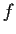
be an infinitely differentiable function from
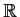
to
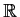
. Suppose that, for some positive integer
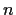
,
Prove that
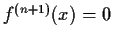
for some
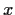
in
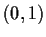
.
Problem 14
Let
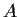
and
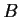
be subspaces of a finite-dimensional vector space
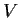
such
that
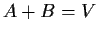
. Write
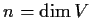
,
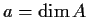
, and
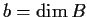
.
Let
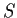
be the set of those
endomorphisms
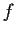
of
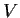
for which
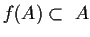
and
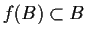
. Prove that
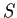
is a subspace of the set of
all endomorphisms of
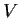
, and express the dimension of
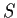
in terms of
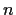
,
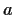
, and
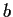
.
Problem 15
Find a one-to-one conformal map of the semidisc
onto the upper half-plane.
Problem 16
Determine the greatest common divisor of the elements of the set
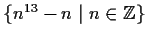
.
Problem 17
Let
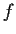
be a differentiable function on
![$[0,1]$](img99-31.gif)
and let
Let
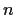
be a positive integer. Prove that
Problem 18
Let
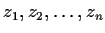
be complex numbers. Prove that there exists
a subset
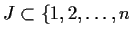
}
such that



Previous: Fall89
Next: Fall90
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10