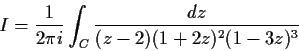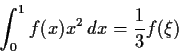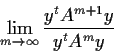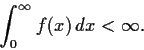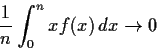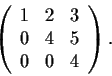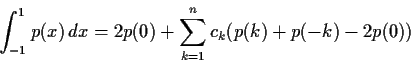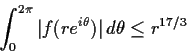Previous: Spring90
Next: Spring91
Preliminary Exam - Fall 1990
Problem 1
Find all pairs of integers
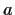
and
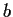
satisfying
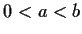
and
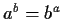
.
Problem 2
Evaluate the integral
where
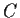
is the circle
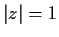
with counterclockwise orientation.
Problem 3
Let
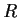
be a ring with
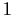
, and let
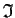
be the left ideal of
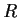
generated by
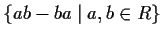
. Prove that
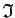
is a two-sided ideal.
Problem 4
Suppose
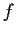
is a continuous real valued function. Show that
for some
![$\xi\in [0,1]$](img16-35.gif)
.
Problem 5
Let
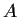
be a real symmetric
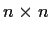
matrix that is positive definite.
Let
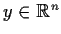
,
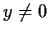
. Prove that the limit
exists and is an eigenvalue of
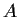
.
Problem 6
Let the function
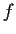
be analytic in the entire complex plane, and
suppose that
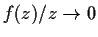
as
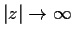
. Prove that
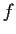
is constant.
Problem 7
Let
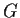
be a group and
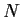
be a normal subgroup of
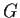
with
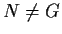
.
Suppose that there does not exist a subgroup
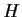
of
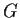
satisfying
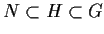
and
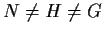
. Prove that the index of
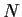
in
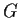
is finite and equal to a prime number.
Problem 8
Let
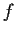
be a continuous real valued function satisfying
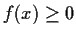
, for all x, and
Prove that
as
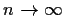
.
Problem 9
Let
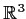
be 3-space with the usual inner product, and
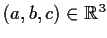
a vector of length
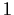
. Let
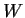
be the plane defined by
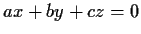
. Find, in the standard basis, the matrix representing
the orthogonal projection of
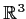
onto
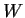
.
Problem 10
Determine the Jordan Canonical Form of the matrix
Problem 11
Suppose that
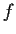
maps the compact interval
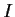
into itself and that
for all
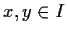
,
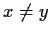
. Can one conclude that there
is some constant
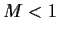
such that, for all
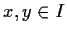
,
Problem 12
Let
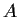
be an additively written abelian group, and
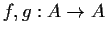
two group homomorphisms. Define the group homomorphisms
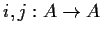
by
Prove that the kernel of i is isomorphic to the kernel of j.
Problem 13
Suppose that
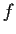
is analytic on the open upper half-plane and
satisfies
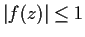
for all
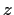
,
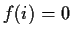
. How large can
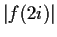
be under these conditions?
Problem 14
Prove that
![$\sqrt{2}+\sqrt[3]{3}$](img67-35.gif)
is irrational.
Problem 15
Let
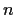
be a positive integer and let
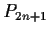
be the vector space
of real polynomials whose degrees are, at most,
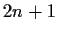
. Prove that
there exist unique real numbers
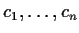
such that
for all
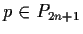
.
Problem 16
Evaluate the limit
Problem 17
Does the set
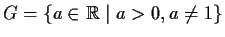
form a group
with the operation
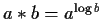
?
Problem 18
Let the function
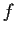
be analytic in the entire complex plane and
satisfy
for all
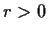
. Prove that
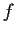
is the zero function.



Previous: Spring90
Next: Spring91
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10