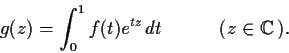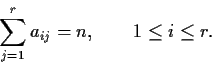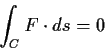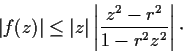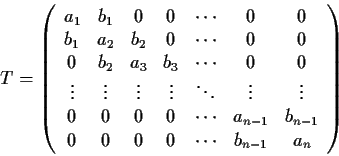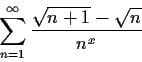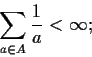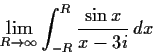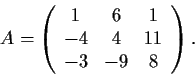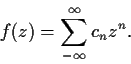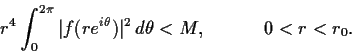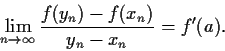Previous: Fall90
Next: Fall91
Preliminary Exam - Spring 1991
Problem 1
List, to within isomorphism, all the finite groups whose orders do not
exceed
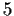
. Explain why your list is complete and why no two
groups on the list are isomorphic.
Problem 2
Let
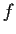
be a continuous complex valued function on
![$[0,1]$](img3-37.gif)
, and
define the function
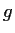
by
Prove that
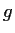
is analytic in the entire complex plane.
Problem 3
For
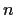
a positive integer, let
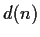
denote the number of
positive integers that divide
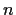
. Prove that
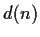
is odd
if and only if n is a perfect square.
Problem 4
Let
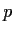
be a prime number and
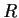
a ring with identity containing
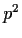
elements. Prove that
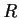
is commutative.
Problem 6
Let the vector field
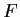
in
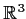
have the form
where
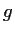
is a real valued smooth function on
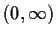
and
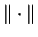
denotes the Euclidean norm. (
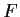
is undefined
at
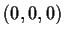
.) Prove that
for any smooth closed path
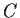
in
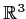
that does not pass
through the origin.
Problem 7
Let the function
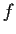
be analytic in the unit disc, with
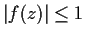
and
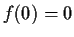
. Assume that there is a number
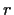
in
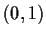
such that
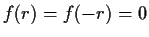
. Prove that
Problem 8
Let
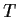
be a real, symmetric,
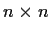
,
tridiagonal matrix:
(All entries not on the main diagonal or the diagonals just above
and below the main one are zero.) Assume
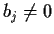
for all
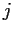
.
_matrix,>tridiagonal
Prove:
-
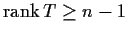 .
.
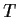 has
has 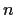 distinct eigenvalues.
distinct eigenvalues.
Problem 9
Let
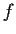
be a continuous function from the ball
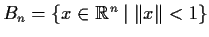
into itself. (Here,
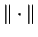
denotes the Euclidean
norm.) Assume
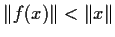
for all nonzero
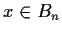
. Let
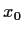
be a nonzero point of
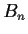
, and define the sequence
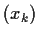
by setting
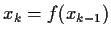
. Prove
that
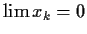
.
Problem 10
Prove that
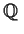
, the additive group of rational numbers, cannot be
written as the direct sum of two nontrivial subgroups.
Note: See also Problems ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) and
and ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 11
For which real numbers x does the infinite series
converge?
Problem 12
Let
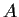
be the set of positive integers that do not contain the
digit
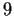
in their decimal expansions. Prove that
that is,
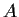
defines a convergent subseries of the harmonic series.
Problem 13
Prove that
exists and find its value.
Problem 14
Let
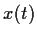
be a nontrivial solution to the system
where
Prove that
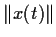
is an increasing function of t. (Here,
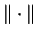
denotes the Euclidean norm.)
Problem 15
Let
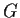
be a finite nontrivial group with the property that for
any two elements
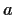
and
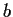
in
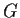
different from the identity,
there is an element
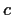
in
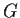
such that
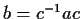
. Prove
that
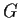
has order
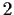
.
Problem 16
Let
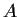
be a linear transformation on an n-dimensional vector
space over
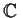
with characteristic polynomial
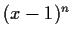
. Prove that
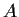
is similar to
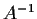
.
Problem 17
Let the function
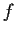
be analytic in the punctured disc
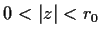
, with Laurent series
Assume there is a positive number
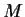
such that
Prove that
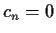
for
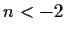
.
Problem 18
Let the real valued function
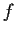
be defined in an open interval
about the point
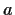
on the real line and be differentiable at
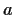
.
Prove that if
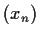
is an increasing sequence and
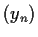
is a decreasing sequence in the domain of
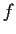
, and both sequences converge to
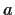
, then



Previous: Fall90
Next: Fall91
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10