


Previous: Spring91
Next: Spring92
Preliminary Exam - Fall 1991
Problem 1
Prove that every finite group of order at least
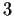
has a
nontrivial automorphism.
Problem 2
Let
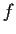
be a continuous function from
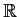
to
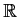
such that
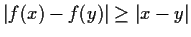
for all
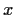
and
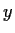
. Prove that the
range of
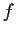
is all of
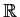
.
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 3
Evaluate the integral
where n is a positive integer, and
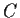
is the circle
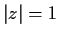
, with
counterclockwise orientation.
Problem 5
Let
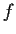
be an infinitely differentiable function from
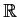
to
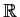
. Suppose that, for some positive integer
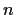
,
Prove that
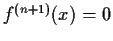 for some
for some 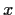 in
in 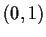 .
.
Problem 6
Let the function f be analytic in the disc
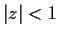
of the complex
plane. Assume that there is a positive constant
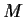
such that
Prove that
Problem 7
Consider the vector differential equation
where
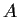
is a smooth
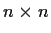
function on
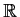
. Assume
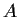
has
the property that
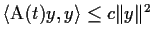
for all
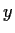
in
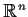
and all
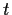
, where
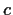
is a fixed real
number. Prove that any solution
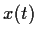
of the equation satisfies
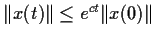
for all
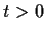
.
Problem 8
Let
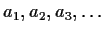
be positive numbers.
- Prove that
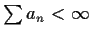 implies
implies
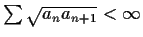 .
.
- Prove that the converse of the above statement is false.
Problem 9
Let
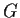
be a group of order
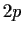
, where
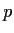
is an odd prime. Assume
that
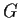
has a normal subgroup of order
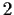
. Prove that
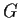
is cyclic.
Problem 10
Let
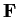
be a finite field of order
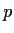
. Compute the order of
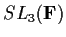
,
the group of 3
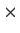
3 matrices over
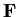
of determinant
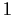
.
Problem 11
Let
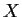
and
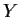
be metric spaces and
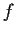
a continuous map of
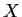
into
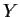
. Let
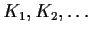
be nonempty compact subsets of
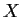
such that
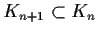
for all
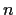
, and let
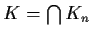
. Prove that
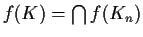
.
Problem 12
Let
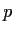
be a nonconstant complex polynomial whose zeros are all in the
half-plane
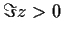
.
- Prove that
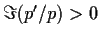 on the real axis.
on the real axis.
- Find a relation between
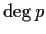 and
and
Problem 13
Let
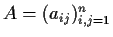
be a real
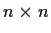
matrix with
nonnegative entries such that
Prove that no eigenvalue of
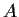
has absolute value greater
than
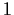
.
Problem 14
Let
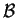
denote the unit ball of
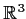
,
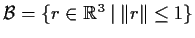
.
Let
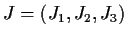
be a smooth vector field on
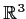
that vanishes
outside of
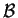
and satisfies
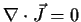
.
- For
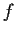 a smooth, scalar-valued function defined on a
neighborhood of
a smooth, scalar-valued function defined on a
neighborhood of 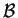 , prove that
, prove that
- Prove that
Problem 15
Let
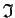
be the ideal in the ring
![% latex2html id marker 1070
$\mbox{$\mathbb{Z}^{}$}[x]$](img95-34.gif)
generated by
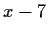
and
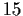
. Prove that the quotient ring
![% latex2html id marker 1078
$\mbox{$\mathbb{Z}^{}$}[x]/\mathfrak{I}$](img98-34.gif)
is isomorphic to
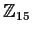
.
Problem 16
Let
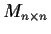
be the space of real n
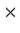
n matrices. Regard it
as a metric space with the distance function
Prove that the set of nilpotent matrices in
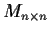 is a closed set.
is a closed set.
Problem 17
Let
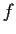
be a
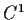
function from the interval
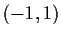
into
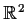
such that
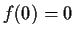
and
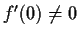
. Prove that there is
a number
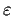
in
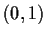
such that
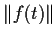
is an
increasing function of
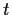
on
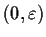
.
Problem 18
Let the function
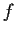
be analytic in the entire complex plane and
satisfy the inequality
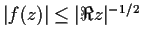
off
the imaginary axis. Prove that
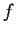
is constant.



Previous: Spring91
Next: Spring92
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



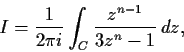
![]() for some
for some ![]() in
in ![]() .
.
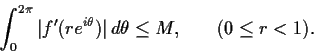
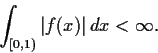
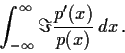
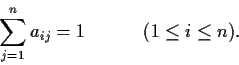
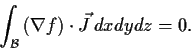
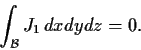
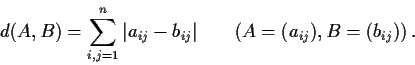
![]() is a closed set.
is a closed set.


