


Previous: Fall91
Next: Fall92
Preliminary Exam - Spring 1992
Problem 2
Find a square root of the matrix
How many square roots does this matrix have?
Problem 3
Let
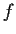
be an analytic function in the connected open subset
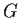
of
the complex plane. Assume that for each point
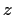
in
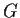
, there is a
positive integer
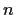
such that the
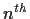
derivative
of
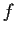
vanishes at
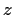
. Prove that
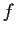
is a polynomial.
Problem 4
Show that every infinite closed subset of
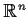
is the closure
of a countable set.
Problem 5
Let
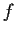
be a differentiable function from
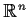
to
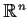
. Assume that
there is a differentiable function
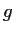
from
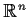
to
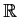
having
no critical points such that
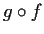
vanishes identically.
Prove that the Jacobian determinant of
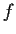
vanishes identically.
Problem 6
Let
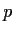
be a prime integer,
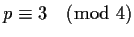
, and let
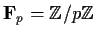
. If
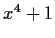
factors into a product
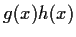
of two quadratic polynomials in
![% latex2html id marker 824
$\mbox{\bf {F}}_p[x]$](img29-39.gif)
, prove that
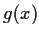
and
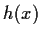
are both irreducible over
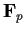
.
Problem 7
Let
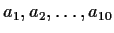
be integers with
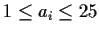
,
for
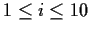
. Prove that there exist integers
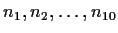
, not all zero, such that
Problem 8
Evaluate the integral
Problem 9
Let
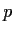
be a nonconstant polynomial with real coefficients and only
real roots. Prove that for each real number
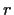
, the polynomial
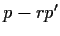
has only real roots.
Problem 10
Let
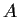
denote the matrix
For which positive integers
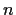
is there a complex 4
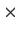
4
matrix
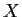
such that
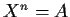
?
Problem 11
Find a Laurent series that converges in the annulus
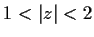
to a
branch of the function
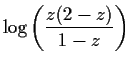
.
Problem 12
Let
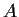
be a real symmetric
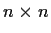
matrix with nonnegative entries.
Prove that
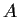
has an eigenvector with nonnegative entries.
Problem 13
Let
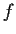
be a one-to-one
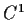
map of
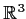
into
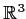
, and let
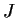
denote its Jacobian determinant. Prove that if
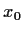
is any
point of
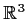
and
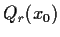
denotes the cube with center
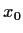
, side length
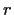
, and edges parallel to the coordinate
axes, then
Here, 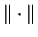 is the Euclidean norm in
is the Euclidean norm in
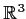 .
.
Problem 15
Let
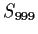
denote the group of all permutations of
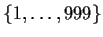
, and let
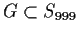
be an abelian
subgroup of order
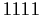
. Prove that there exists
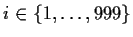
such that for all
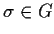
, one has
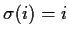
.
Problem 16
Let
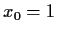
and
Prove that
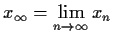
exists, and find its value.
Problem 17
For which positive numbers
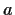
and
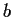
, with
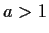
, does the
equation
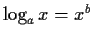
have a positive solution for
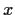
?
Problem 18
Let the function
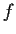
be analytic in the entire complex plane,
real valued on the real axis, and of positive imaginary part in
the upper half-plane. Prove
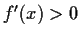
for
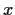
real.



Previous: Fall91
Next: Fall92
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
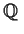 , the
additive group of rational numbers, is cyclic.
, the
additive group of rational numbers, is cyclic.
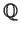 /
/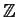 , where
, where 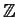 is the group of integers?
is the group of integers?



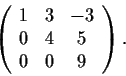
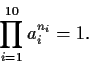
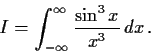
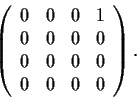
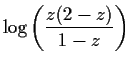 .
.
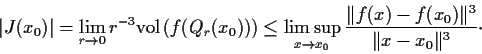
![]() is the Euclidean norm in
is the Euclidean norm in
![]() .
.


