


Previous: Spring92
Next: Spring93
Preliminary Exam - Fall 1992
Problem 1
Are the matrices
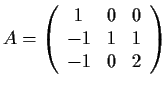
and
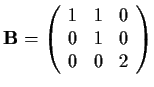
similar?
Problem 2
Let
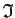
denote the ideal in
![% latex2html id marker 681
$\mathbb{Z}[x]$](img4-40.gif)
, the ring of
polynomials with coefficients in
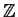
, generated by
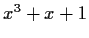
and
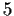
.
Is
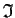
a prime ideal?
Problem 3
- How many roots does the polynomial
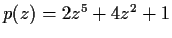 have in the disc
have in the disc 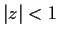 ?
?
- How many roots does the same polynomial have on the real axis?
Problem 4
Let the real valued function
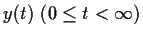
solve the initial value problem
Prove that there is exactly one
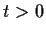
such that
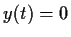
.
Problem 5
Let
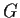
be a group and
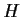
and
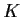
subgroups such that
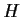
has a finite index in
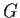
. Prove that
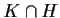
has a finite index in
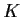
.
Problem 6
Let
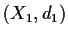
and
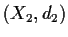
be metric spaces and
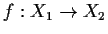
a continuous surjective map such that
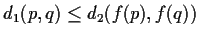
for every pair of points
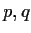
in
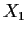
.
- If
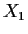 is complete, must
is complete, must 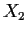 be complete? Give a proof or a
counterexample.
be complete? Give a proof or a
counterexample.
- If
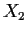 is complete, must
is complete, must 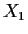 be complete? Give a proof or a
counterexample.
be complete? Give a proof or a
counterexample.
Problem 7
Evaluate
where
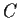
is the unit circle with counterclockwise orientation.
Problem 9
Let the function
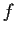
be analytic in the region
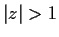
of the complex plane. Prove that if
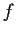
is real valued on the interval
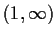
of the real axis, then
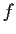
is also real valued on the interval
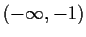
.
Problem 10
How many Sylow
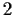
-subgroups does the dihedral group
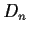
of
order
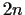
have, when
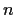
is odd?
Problem 11
Let
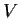
be a finite-dimensional vector space over a field
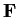
,
and let
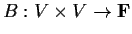
be a bilinear map (not necessarily symmetric).
Define the subspaces
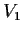
and
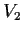
by
Prove that
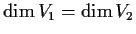
.
Problem 12
Let
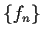
be a sequence of real valued
functions on
![$[0,1]$](img70-40.gif)
such that, for all n,
Prove that the sequence has a subsequence that converges uniformly on ![$[0,1]$](img73-40.gif) .
.
Problem 14
Let
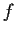
and
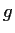
be positive continuous functions on
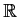
,
with
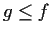
everywhere. Assume the initial value problem
has a solution defined on all of
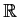
. Prove that the initial value problem
also has a solution defined on all of
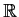
.
Problem 15
Let
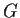
be the group of all real 2
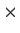
2 matrices of the
form
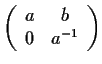
with
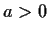
. Let
be the subgroup of those matrices in
having
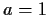
.
(a) Prove that 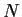 is a normal subgroup of
is a normal subgroup of 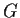 and that
and that 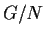 is isomorphic to
is isomorphic to
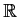 .
.
(b) Find a proper normal subgroup of 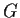 that contains
that contains 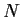 properly.
properly.
Problem 16
Let f be a
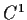
function of
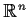
into
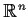
such that
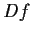
has rank
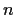
everywhere. Assume
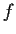
is proper (which, by
definition, means
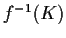
is compact whenever
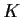
is compact). Prove that
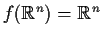
.
Problem 17
Let
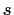
be a real number, and let the function
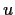
be
defined in
![% latex2html id marker 1080
$\mathbb{C}\backslash (- \infty, 0]$](img107-25.gif)
by
Prove that
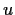
is a harmonic function.
Problem 18
Let
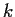
be a positive integer. Determine those real numbers
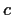
for which every sequence
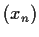
of real numbers satisfying the
recurrence relation
has period k (i.e.,
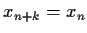
for all n).



Previous: Spring92
Next: Spring93
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10
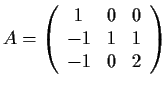 and
and
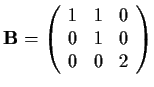 similar?
similar?



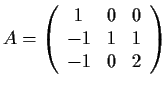 and
and
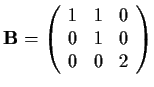 similar?
similar?
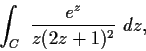
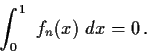
![]() .
.
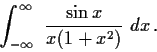
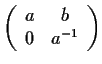 with
with ![]() is a normal subgroup of
is a normal subgroup of ![]() and that
and that ![]() is isomorphic to
is isomorphic to
![]() .
.
![]() that contains
that contains ![]() properly.
properly.


