


Previous: Fall92
Next: Fall93
Preliminary Exam - Spring 1993
Problem 1
Let
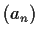
and
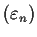
be sequences of positive numbers. Assume that
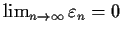
and that there is a number
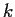
in
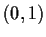
such that
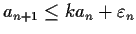
for every
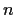
. Prove that
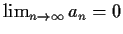
.
Problem 2
Let
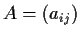
be an
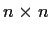
matrix such that
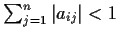
for each
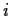
. Prove that
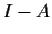
is invertible.
Problem 4
Suppose that the group
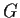
is generated by elements
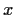
and
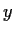
that satisfy
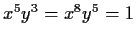
. Does it follow that
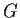
is the trivial group?
Problem 5
Let
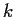
be a positive integer. For which values of the real number
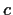
does
the differential equation
have a solution satisfying
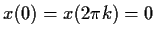
?
Problem 6
Find a list of real matrices, as long as possible, such that
- the characteristic polynomial of each matrix is
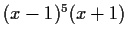 ,
,
- the minimal polynomial of each matrix is
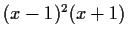 ,
,
- no two matrices in the list are similar to each other.
Problem 8
Classify up to isomorphism all groups of order
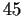
.
Problem 9
Let

be a complex number and
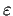
a positive number.
Prove that the function
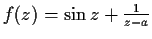
has
infinitely many zeros in the strip
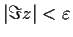
.
Problem 10
Let
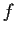
be a real valued
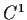
function on
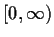
such that
the improper integral
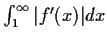
converges. Prove that the
infinite series
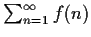
converges if and only if
the integral
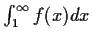
converges.
Problem 11
Let
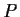
be the vector space of polynomials over
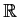
. Let
the linear transformation
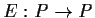
be defined by
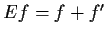
, where
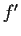
is the derivative of
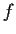
. Prove that
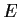
is invertible.
Problem 12
Prove that for any fixed complex number
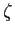
,
Problem 13
Prove that no commutative ring with identity has additive group
isomorphic to
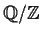
.
Problem 14
Prove that every solution
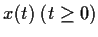
of the
differential equation
with
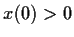
satisfies
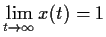
.
Problem 15
Let
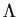
be the set of 2
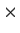
2 matrices of the form
where a and b are elements of a given field
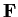
. Prove
that
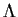
, with the usual matrix operations, is a commutative
ring with identity. For which of the following fields
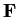
is
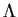
a field?
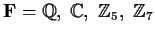
.
Problem 16
Prove that
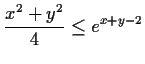
for
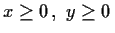
.
Problem 17
Prove that if
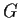
is a group containing no subgroup of index
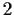
,
then any subgroup of index
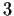
in
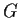
is a normal subgroup.



Previous: Fall92
Next: Fall93
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



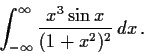
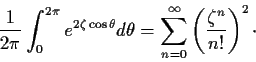
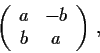
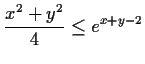 for
for


