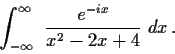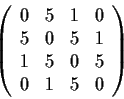Previous: Spring93
Next: Spring94
Preliminary Exam - Fall 1993
Problem 1
Let
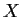
be a metric space and
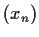
a convergent sequence in
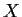
with limit

. Prove
that the set
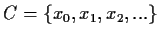
is compact.
Problem 2
Let
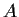
be the additive group of rational
numbers, and let

be the multiplicative group
of positive rational numbers. Determine all homomorphisms
of
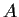
into
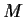
.
Problem 3
Describe the region in the complex plane where the
infinite series
converges. Draw a sketch of the region.
Problem 4
Let
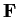
be a field. For
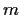
and
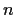
positive integers, let
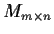
be the vector space of

matrices over

. Fix

and
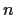
, and fix
matrices
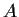
and
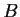
in
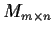
. Define the
linear transformation
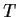
from
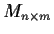
to
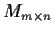
by
Prove that if 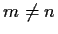 , then
, then 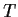 is not invertible.
is not invertible.
Problem 5
Let the function
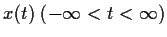
be a
solution of the differential equation
such that
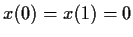
. (Here,
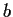
and
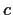
are
real constants.) Prove that

for every integer
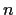
.
Problem 6
Let
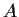
,
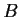
, and
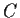
be finite abelian groups.
Prove that if
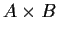
is isomorphic to
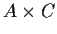
,
then
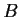
is isomorphic to
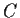
.
Problem 7
Let
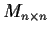
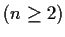
be the space of real
n

n matrices, identified in the usual way with
the Euclidean space
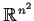
. Let
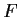
be the
determinant map of
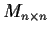
into
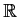
:
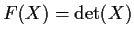
.
Find all of the
critical points of

; that is,
all matrices
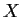
such that
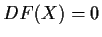
. _function,>critical points
Problem 8
Prove that if
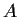
is an

matrix
over
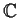
, and if
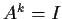
for some positive
integer
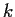
, then
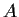
is diagonalizable.
Problem 10
Let
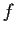
be a continuous real valued function on

. Let
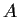
be the set of real numbers
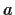
that can be expressed as
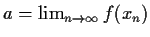
for some
sequence

in
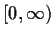
such that
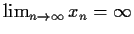
.
Prove that if

contains the two numbers
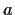
and
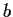
,
then it contains the entire interval with endpoints

and
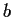
.
Problem 11
Let
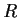
be a commutative ring with identity.
Let
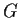
be a finite subgroup of
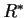
, the group of
units of
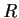
. Prove that if
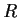
is an integral domain,
then
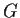
is cyclic.
Problem 12
Evaluate
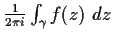
for the function

and the curve
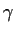
depicted by
file=../Fig/Pr/Fa93-12,width=3.7in
Problem 13
Show that there are at least two nonisomorphic
nonabelian groups of order
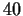
.
Problem 14
Let
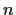
be an integer larger than
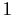
. Is
there a differentiable function on
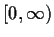
whose
derivative equals its

power and whose value
at the origin is positive?
Problem 15
Prove that the matrix
has two positive and two negative eigenvalues (taking
into account multiplicities).
Problem 16
Let
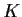
be a continuous real valued function
on
![$[0,1] \times [0,1]$](img89-38.gif)
. Let

be the family of
functions
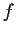
on
![$[0,1]$](img92-37.gif)
of the form
with
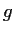
a real valued continuous function on
![$[0,1]$](img95-36.gif)
satisfying
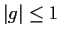
everywhere. Prove that the
family

is equicontinuous.
Problem 18
Let
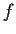
be a continuous real valued function
on
![$[0,1]$](img118-13.gif)
, and let the function
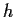
in the complex
plane be defined by
- Prove that
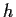 is analytic in the entire plane.
is analytic in the entire plane.
- Prove that
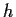 is the zero function only if
is the zero function only if
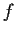 is the zero function.
is the zero function.



Previous: Spring93
Next: Spring94
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



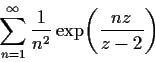
![]() , then
, then ![]() is not invertible.
is not invertible.