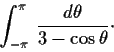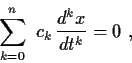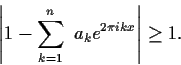Previous: Fall93
Next: Fall94
Preliminary Exam - Spring 1994
Problem 1
Let the collection
of open subsets of
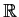
cover the
interval
![$[0,1]$](img3-43.gif)
. Prove that there is a positive number
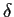
such that any two points
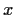
and
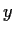
of
![$[0,1]$](img7-43.gif)
satisfying

belong together to some member of the cover

.
Problem 4
Let
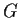
be a group having a subgroup
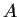
of finite
index. Prove that there is a normal subgroup
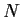
of
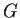
contained in
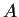
such that
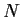
is of finite index in
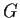
.
Problem 6
Prove or disprove: A square complex matrix,
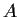
, is similar to its
transpose,
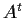
.
Problem 7
Let

be complex numbers. Prove that
there is a point
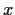
in
![$[0,1]$](img37-43.gif)
such that
Problem 8
Find all automorphisms of
![% latex2html id marker 789
$\mathbb{Z}[x]$](img39-43.gif)
, the ring of
polynomials over
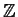
.
Problem 9
- Let
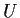 and
and  be open connected subsets of
the complex plane, and let
be open connected subsets of
the complex plane, and let 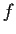 be an analytic function
in
be an analytic function
in  such that
such that
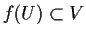 . Assume
. Assume 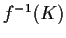 is
compact whenever
is
compact whenever 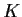 is a compact subset of
is a compact subset of 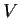 . Prove
that
. Prove
that 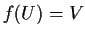 .
.
- Prove that the last equality can fail if analytic
is replaced by continuous in the preceding statement.
Problem 10
Let f be a continuous real valued function on

such that the improper Riemann integral
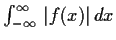
converges. Define the function g on
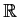
by
Prove that g is continuous.
Problem 11
Let
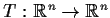
be a diagonalizable
linear transformation. Prove that there is an orthonormal basis
for
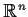
with respect to which
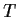
has an upper-triangular
matrix.
Problem 12
Let
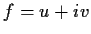
and
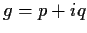
be analytic functions
defined in a neighborhood of the origin in the complex
plane. Assume
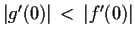
. Prove that there is
a neighborhood of the origin in which the function
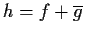
is one-to-one.
Problem 13
Let
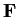
be a finite field with q elements.
Say that a function
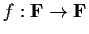
is a
polynomial
function if there are elements
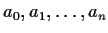
of

such
that
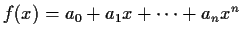
for all
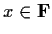
.
How many polynomial functions are there? _function,>polynomial
Problem 14
Let
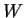
be a real 3
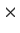
3 antisymmetric matrix, i.e.,
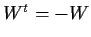
. Let the function
be a real solution of the vector differential equation
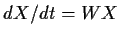
.
- Prove that
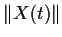 , the Euclidean norm of
, the Euclidean norm of 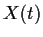 , is
independent of
, is
independent of 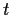 .
.
- Prove that if
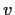 is a vector in the null space of
is a vector in the null space of 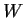 ,
then
,
then 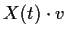 is independent of
is independent of 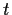 .
.
- Prove that the values
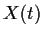 all lie on a fixed circle in
all lie on a fixed circle in 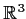 .
.
Problem 15
Let
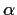
be a number in
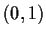
. Prove that any
sequence
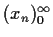
of real
numbers satisfying the recurrence relation
has a limit, and find an expression for the limit in
terms of
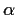
,
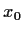
, and
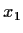
.
Problem 16
For which numbers
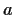
in
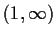
is it true that
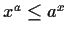
for all

in
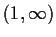
?
Problem 17
Prove that there are at least two nonisomorphic
nonabelian groups of order

.
Problem 18
Let u be a real valued harmonic function
in the complex plane such that
for all z, where a and b are positive constants.
Prove that u is constant.



Previous: Fall93
Next: Fall94
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10