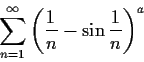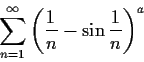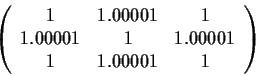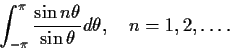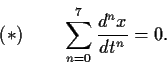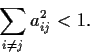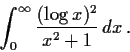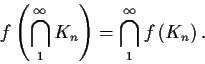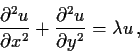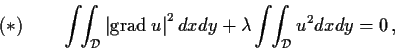Previous: Spring94
Next: Spring95
Preliminary Exam - Fall 1994
Problem 1
For which values of the real number
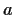
does the series
converge?
Problem 2
Prove that the matrix
has one positive eigenvalue and one negative eigenvalue.
Problem 3
Evaluate the integrals
Problem 4
Suppose the group
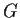
has a nontrivial subgroup
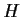
which is
contained in every nontrivial subgroup of
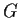
. Prove that
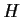
is contained in the center of
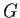
.
Problem 5
- Find a basis for the space of real solutions
of the differential equation
- Find a basis for the subspace of real solutions of
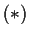 that satisfy
that satisfy
Problem 6
Let
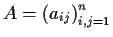
be a real
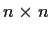
matrix such that
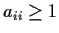
for all
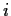
, and
Prove that
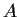
is invertible.
Problem 7
Let
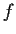
be a continuously differentiable function
from
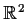
into
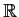
. Prove that
there is a continuous one-to-one function
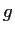
from
![$[0,1]$](img23-44.gif)
into
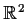
such that the composite function
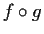
is constant.
Problem 8
Let
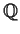
be the field of rational numbers. For
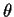
a real number, let
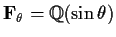
and
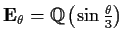
.
Show that
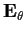
is an extension field of
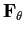
, and determine all possibilities
for
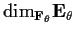
.
Problem 10
Let the function
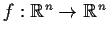
satisfy
the following two conditions:
- (i)
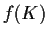 is compact whenever
is compact whenever 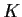 is a compact subset of
is a compact subset of
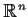 .
.
- (ii)
- If
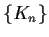 is a decreasing
sequence of compact subsets of
is a decreasing
sequence of compact subsets of
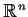 , then
, then
Prove that
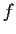
is continuous.
Problem 11
Write down a list of 5
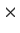
5 complex matrices, as long as possible,
with the following properties:
- The characteristic polynomial of each matrix in the list is
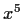 ;
;
- The minimal polynomial of each matrix in the list is
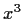 ;
;
- No two matrices in the list are similar.
Problem 12
Suppose the coefficients of the power series
are given by the recurrence relation
Find the radius of convergence of the series and the function to which
it converges in its disc of convergence.
Problem 13
Let
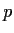
be an odd prime and
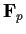
the field of
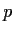
elements.
How many elements of
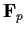
have square roots in
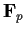
?
How many have cube roots in
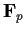
?
Problem 14
Find the maximum area of all triangles that can be inscribed in an ellipse
with semiaxes
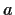
and
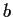
, and describe the triangles that have maximum area.
Note: See also Problem ![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif) .
.
Problem 15
Let
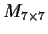
denote the vector space of real 7
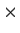
7 matrices. Let
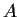
be a diagonal matrix in
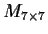
that has
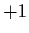
in four diagonal positions and
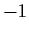
in three diagonal positions. Define the linear transformation
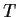
on
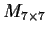
by
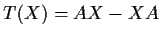
. What is the dimension of the range of
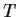
?
Problem 16
Let
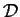
denote the open unit disc in
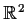
. Let
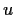
be an
eigenfunction for the Laplacian in
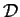
; that is,
a real valued function of class
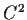
defined in
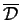
,
zero on the boundary of
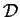
but not identically zero, and
satisfying the differential equation _Laplacian,>eigenfunction
where
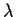
is a constant. Prove that
and hence that
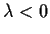
.
Problem 17
Let
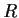
be a ring with identity, and let
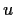
be an element of
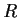
with a right inverse. Prove that the following conditions on
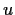
are
equivalent:
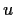 has more than one right inverse;
has more than one right inverse;
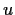 is a zero divisor;
is a zero divisor;
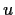 is not a unit.
is not a unit.
Problem 18
Let the function
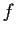
be analytic in the complex plane, real on the real
axis,
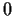
at the origin, and not identically
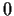
. Prove that if
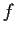
maps the imaginary axis into a straight line, then that straight line
must be either the real axis or the imaginary axis.



Previous: Spring94
Next: Spring95
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10