


Previous: Fall94
Next: Fall95
Preliminary Exam - Spring 1995
Problem 1
For each positive integer
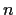
, define
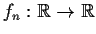
by
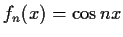
. Prove that the sequence of functions
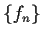
has no uniformly convergent subsequence.
Problem 2
Let
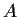
be the 3
3 matrix
Determine all real numbers a for which the limit

exists and is nonzero (as a matrix).
Problem 3
Let n be a positive integer and

. Prove that
where the circle
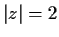
is oriented counterclockwise.
Problem 5
Let
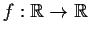 be a bounded continuously differentiable function.
Show that every solution of
be a bounded continuously differentiable function.
Show that every solution of
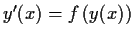 is monotone.
is monotone.
Problem 6
Suppose that
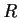
is a subring of a commutative ring
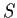
and that
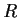
is of
finite index
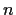
in

. Let
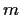
be an integer that is relatively prime
to
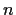
. Prove that the natural map

is a ring isomorphism.
Problem 7
Let 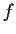 ,
,
![$g\colon[0,1]\to[0,\infty)$](img33-46.gif) be continuous functions satisfying
be continuous functions satisfying
Prove that there exists
![$t\in[0,1]$](img35-46.gif)
with

.
Problem 8
Suppose that
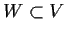
are finite-dimensional vector spaces over a field,
and let
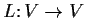
be a linear transformation with
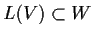
.
Denote the restriction of
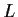
to

by
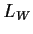
. Prove that
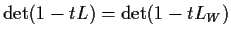
.
Problem 10
Let
![$f_n\colon[0,1]\to[0,\infty)$](img49-46.gif)
be a continuous function, for
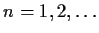
. Suppose that one has
Let

and
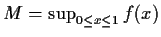
.
- Prove that there exists
![$t\in[0,1]$](img54-46.gif) with
with 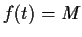 .
.
- Show by example that the conclusion of Part 1 need not hold if
instead of
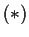 we merely know that for each
we merely know that for each ![$x\in[0,1]$](img57-46.gif) there exists
there exists 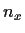 such that for all
such that for all 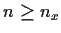 one has
one has
 .
.
Problem 11
Let
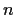
be a positive integer, and let
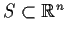
a finite subset
with
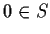
. Suppose that
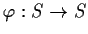
is a map satisfying
where
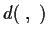
denotes Euclidean distance. Prove that
there is a linear map
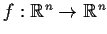
whose restriction to
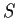
is
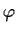
.
Problem 12
Let
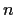
be a positive integer. Compute
Problem 15
Let
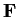
be a finite field, and suppose that the subfield of
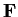
generated by
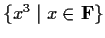
is different from
. Show that
has cardinality
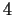
.
Problem 16
Let  be a nonempty compact set in a metric space with distance
function
be a nonempty compact set in a metric space with distance
function 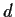 . Suppose that
. Suppose that
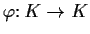 satisfies
satisfies
for all
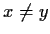
in
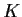
. Show there exists precisely one point

such
that
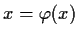
.
Problem 17
Let
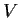
be a finite-dimensional vector space over a field
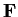
, and let
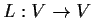
be a linear transformation. Suppose that the characteristic
polynomial
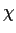
of
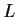
is written as
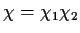
, where
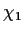
and
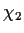
are two relatively prime polynomials with coefficients in
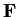
.
Show that
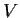
can be written as the direct sum of two subspaces
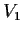
and
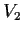
with the property that
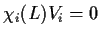
for
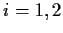
.
Problem 18
Prove that there is no one-to-one conformal map of the punctured disc

onto the
annulus

.



Previous: Fall94
Next: Fall95
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



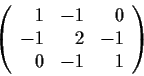
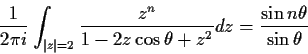
![]() be a finite field of cardinality
be a finite field of cardinality ![]() , with p prime and
, with p prime and ![]() ,
and let
,
and let ![]() be the group of invertible 2
be the group of invertible 2![]() 2 matrices with coefficients
in
2 matrices with coefficients
in
![]() .
.
![]() be a bounded continuously differentiable function.
Show that every solution of
be a bounded continuously differentiable function.
Show that every solution of
![]() is monotone.
is monotone.
![]() ,
,
![]() be continuous functions satisfying
be continuous functions satisfying
![]() be a polynomial with real coefficients and with leading
coefficient
be a polynomial with real coefficients and with leading
coefficient ![]() . Suppose that
. Suppose that ![]() and that
and that ![]() has no complex
zeros inside the unit circle. Prove that
has no complex
zeros inside the unit circle. Prove that ![]() .
.
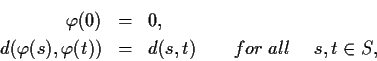
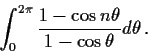
![]() be an odd positive integer, and denote by
be an odd positive integer, and denote by ![]() the group of all
permutations of
the group of all
permutations of
![]() . Suppose that
. Suppose that ![]() is a subgroup of
is a subgroup of ![]() of
of ![]() -power order. Prove that there exists
-power order. Prove that there exists
![]() such that
for all
such that
for all ![]() , one has
, one has ![]() .
.
![]() be a three times differentiable function satisfying
the differential equation
be a three times differentiable function satisfying
the differential equation ![]() . Suppose that
. Suppose that
![]() .
Find real numbers
.
Find real numbers ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , not all zero, such that
, not all zero, such that
![]() .
.
![]() be a nonempty compact set in a metric space with distance
function
be a nonempty compact set in a metric space with distance
function ![]() . Suppose that
. Suppose that
![]() satisfies
satisfies


