


Previous: Spring95
Next: Spring96
Preliminary Exam - Fall 1995
Problem 1
Let
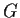
be a group generated by
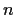
elements. Find an upper bound
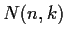
for the number of subgroups
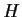
of
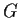
with the index
![$[G:H]=k$](img6-45.gif)
.
Problem 2
Let
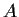
be a finite subset of the unit disc in the plane,
and let
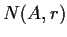
be the set of points at distance
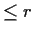
from
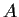
, where
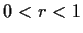
. Show that the length of the
boundary
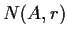
is, at most,
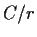
for some constant
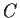
independent of
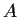
.
Problem 3
Find the radius of convergence
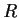
of the Taylor series about
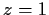
of the function
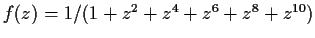
.
Express your answer in terms of real numbers and square roots only.
Problem 4
Suppose
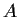
and
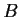
are real
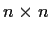
matrices and
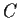
is a complex
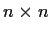
matrix such that
Find a real
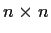
matrix
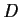
such that
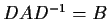
.
Problem 5
Prove that
![% latex2html id marker 738
$\mbox{$\mathbb{Q}\,^{}$}[x,y]/\langle x^2+y^2-1 \rangle$](img28-45.gif)
is an integral domain and
that its field of fractions is isomorphic to the field of
rational functions
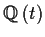
.
Problem 6
Determine all real numbers
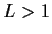
so that the boundary value problem
has a nonzero solution.
Problem 7
Let
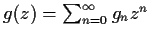
and
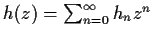
be entire functions.
Find a formula for the coefficients
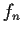
in the Taylor
expansion about
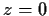
of
Problem 8
Show that an
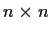
matrix of complex numbers
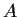
satisfying
for
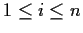
must be invertible.
Problem 9
Let
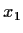
be a real number,
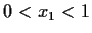
, and define a sequence by
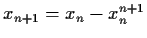
. Show that
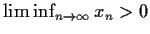
.
Problem 10
Let
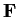
be a field and
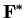
be the multiplicative group of
nonzero elements. Let
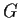
be a subgroup of
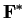
of
finite order
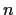
. Show that
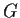
is cyclic.
Problem 11
Let
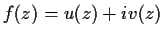
be holomorphic in
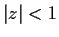
,
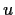
and
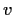
real. Show that
for
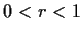
if
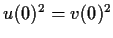
.
Problem 12
Let
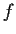
and
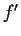
be continuous on
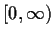
and
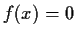
for
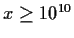
. Show that
Problem 13
Show that
for
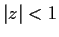
.
Problem 14
Let
![% latex2html id marker 911
$f(x)\in \mbox{$\mathbb{Q}\,^{}$}[x]$](img67-45.gif)
be a polynomial with rational coefficients.
Show that there is a
![% latex2html id marker 915
$g(x)\in \mbox{$\mathbb{Q}\,^{}$}[x]$](img68-45.gif)
,
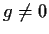
, such that
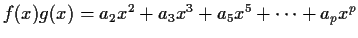
is a polynomial in which only prime exponents appear.
Problem 15
Let
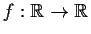
be a
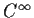
function. Assume that
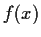
has a
local minimum at
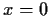
. Prove there is a disc centered on the
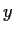
axis which lies above the graph of
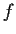
and touches the graph at
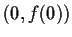
.
Problem 16
Let
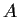
and
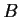
be nonsimilar
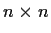
complex matrices with
the same minimal and the same characteristic polynomial.
Show that
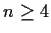
and the minimal polynomial is not equal to
the characteristic polynomial.
Problem 17
Let
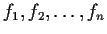
be continuous real valued functions
on
![$[a,b]$](img83-43.gif)
. Show that the set
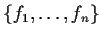
is
linearly dependent on
![$[a,b]$](img85-42.gif)
if and only if
Problem 18
Let
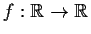
be a nonzero
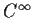
function such that
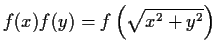
for all
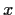
and
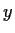
and
that
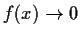
as
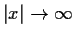
.
- Prove that
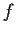 is an even function and that
is an even function and that 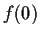 is
is 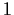 .
.
- Prove that
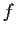 satisfies the differential equation
satisfies the differential equation
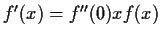 , and find the most general function satisfying
the given conditions.
, and find the most general function satisfying
the given conditions.



Previous: Spring95
Next: Spring96
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



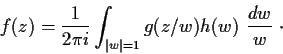
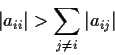
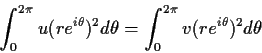
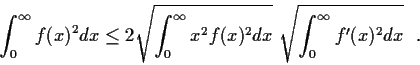
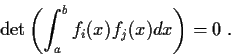
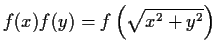 for all
for all 

