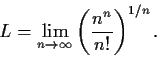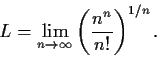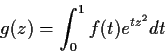Previous: Fall95
Next: Fall96
Preliminary Exam - Spring 1996
Problem 2
Let
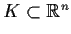
be compact and
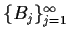
be a sequence of open balls which covers
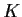
.
Prove that there is
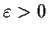
such that every
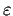
-ball
centered at a point of
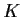
is contained in one of the balls
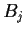
.
Problem 4
Let
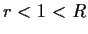
. Show that for all sufficiently small
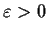
,
the polynomial
has exactly five roots (counted with their multiplicities) inside the annulus
Problem 5
Prove or disprove: For any 2
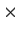
2 matrix
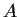
over
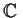
, there
is a 2
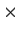
2 matrix
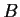
such that
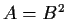
.
Problem 6
If a finite homogeneous system of linear equations with rational coefficients
has a nonzero complex solution, need it have a nonzero rational solution?
Prove or give a counterexample.
Problem 7
Prove that
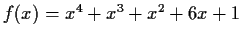
is irreducible over
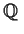
.
Problem 8
Determine the rightmost decimal digit of
Problem 9
Exhibit infinitely many pairwise nonisomorphic quadratic extensions of
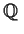
and show they are pairwise nonisomorphic.
Problem 10
Show that a positive constant
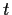
can satisfy
if and only if
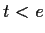
.
Problem 11
Suppose
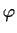
is a
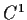
function on
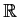
such that
Prove or give a counterexample:
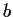
must be zero.
Problem 12
Let
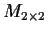
be the space of 2
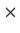
2 matrices over
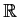
,
identified in the usual way with
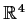
.
Let the function
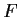
from
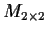
into
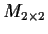
be defined by
Prove that the range of
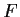
contains a neighborhood of the origin.
Problem 13
Let
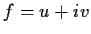
be analytic in
a connected open set
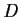
, where
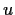
and
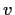
are real valued.
Suppose there are real constants
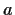
,
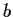
and
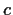
such that
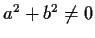
and
in
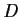
. Show that
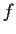
is constant in
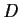
.
Problem 14
Suppose
![% latex2html id marker 894
$f\colon [0,1]\to \mbox{$\mathbb{C}\,^{}$}$](img53-48.gif)
is continuous. Show that
defines a function
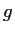
that is analytic everywhere in the complex plane.
Problem 15
Suppose that
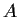
and
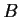
are real matrices such that
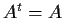
,
for all
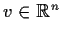
and
Show that
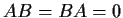
and give an example where neither
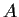
nor
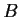
is zero.
Problem 16
Let
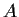
be the
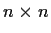
matrix which has zeros on the main diagonal
and ones everywhere else. Find the eigenvalues and eigenspaces of
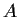
and
compute
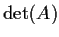
.
Problem 17
Let
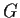
be the group of 2
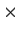
2 matrices with determinant
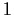
over the four-element field
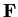
.
Let
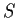
be the set of lines through the origin in
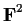
.
Show that
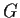
acts
faithfully on
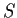
.
(The action is faithful if the only element of
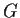
which fixes
every element of
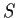
is the identity.) _group action, faithful
Problem 18
Let
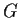
and
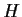
be finite groups of relatively prime orders.
Show that the automorphism group
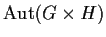
is isomorphic
to the direct product of
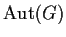
and
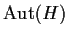
.



Previous: Fall95
Next: Fall96
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10