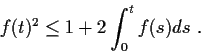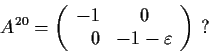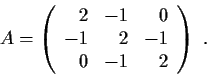Previous: Spring96
Next: Spring97
Preliminary Exam - Fall 1996
Problem 1
Let
be the set of real valued continuous functions
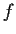
on
![$[0,1]$](img3-47.gif)
such that
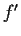
is continuous on
![$[0,1]$](img5-47.gif)
, with the norm
Which subsets of
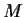
are compact?
Problem 2
A real-valued function
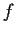
on a closed bounded interval
![$[a,b]$](img9-47.gif)
is said to be upper semicontinuous provided that for every
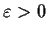
and
![$p\in [a,b]$](img11-47.gif)
, there is a
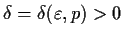
such that if
![$x\in [a,b]$](img13-47.gif)
and
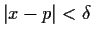
then
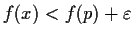
. Prove that an upper semicontinuous function is bounded
above on
![$[a,b]$](img16-47.gif)
.
Problem 3
Evaluate the integral
Problem 4
Does there exist a function
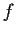
, analytic in the punctured plane
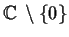
, such that
for all nonzero
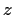
?
Problem 5
Prove that any linear transformation
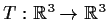
has
- a one-dimensional invariant subspace
- a two-dimensional invariant subspace.
Problem 6
Let
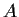
and
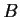
be real 2
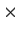
2 matrices such that
Show that there exists a real 2
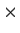
2 matrix
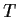
such that
Problem 7
Suppose
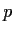
is a prime. Show that every element of
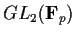
has order
dividing either
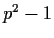
or
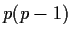
.
Problem 8
Show the denominator of
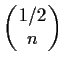
is a power of
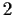
for all integers
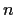
.
Problem 9
For positive integers
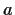
,
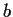
and
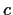
show that
Problem 10
If
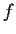
is a
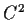
function on an open interval, prove that
Problem 11
Let
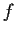
be continuous and nonnegative on
![$[0,1]$](img45-47.gif)
and suppose that
Prove that
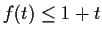
for
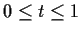
.
Problem 12
Find the number of roots, counted with their multiplicities, of
which lie between the circles
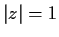
and
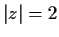
.
Problem 13
Define
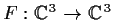
by
Show that
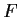
is onto but not one-to-one.
Problem 14
Let
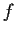
be holomorphic on and inside the unit circle
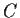
.
Let
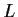
be the length of the image of
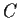
under
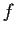
. Show that
Problem 15
Is there a real 2
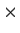
2 matrix
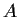
such that
Exhibit such an
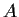
or prove there is none.
Problem 16
Let
Show that every real matrix
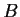
such that
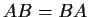
has the form
for some real numbers
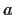
,
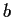
, and
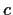
.
Problem 17
Let
![% latex2html id marker 963
$\mbox{$\mathbb{Z}^{}$}[x]$](img72-47.gif)
be the ring of polynomials in the indeterminate
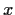
with
coefficients in the ring
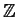
of integers. Let
![% latex2html id marker 971
$\mathfrak{I}\subset \mbox{$\mathbb{Z}^{}$}[x]$](img75-46.gif)
be the ideal generated by
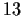
and
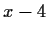
. Find an integer
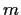
such
that
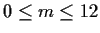
and
Problem 18
Prove that any finite group is isomorphic to
- a subgroup of the group of permutations of
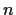 objects
objects
- a subgroup of the group of permutations of
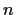 objects which consists only of even permutations.
objects which consists only of even permutations.



Previous: Spring96
Next: Spring97
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10



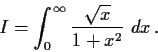
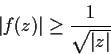
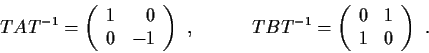
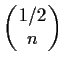 is a power of
is a power of