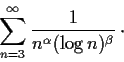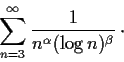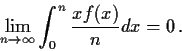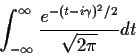Previous: Fall96
Next: Fall97
Preliminary Exam - Spring 1997
Problem 1
For which values of the exponents
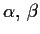
does the
following series converge?
Problem 2
Let

be a metric space with metric
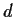
. Let
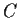
be a
nonempty closed subset of

. Define
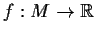
by
Show that
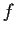
is continuous, and that
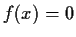
if and
only if
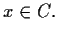
Problem 3
Suppose that
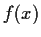
is continuous, nonnegative for
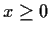
,
with
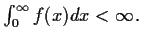
Prove that
Problem 4
Let
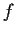
and
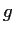
be two entire functions such that, for all
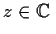
,
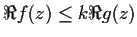
for some real constant
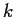
(independent of
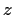
). Show that there are constants

such that
Problem 5
Prove that
is independent of the real parameter
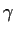
.
Problem 6
Suppose that
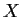
is a topological space and
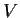
is a finite-dimensional
subspace of the vector space of continuous real valued functions on
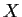
.
Prove that there exist a basis

for
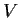
and points
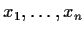
in
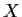
such that
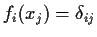
.
Problem 8
Classify all abelian groups of order
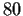
up to isomorphism.
Problem 9
Let
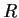
be the ring of
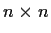
matrices over a field. Suppose

is a ring and
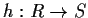
is a homomorphism. Show that
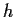
is either
injective or zero.
Problem 10
Let
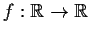
be a bounded function (i.e., there is a constant
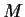
such that
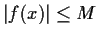
for all

). Suppose the graph
of
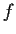
is a closed subset of
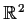
. Prove that
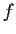
is continuous.
Problem 11
Suppose that
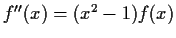
for all
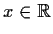
, and that

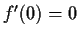
. Show that
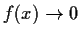
as
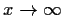
.
Problem 12
Evaluate the integral
Problem 13
Suppose that
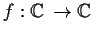
is injective and everywhere holomorphic.
Prove that there exist
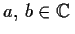
with
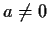
such that
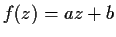
for all
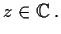
Problem 14
Show that
for any complex
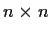
matrix
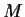
, where

is defined
as in Problem
![[*]](file:/local/sol/2.6/depot/tetex-20000212/lib/latex2html/icons/crossref.gif)
.
Problem 15
Suppose that
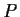
and
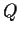
are
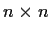
matrices such that
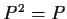
,

, and

is invertible. Show that
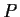
and
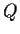
have the same rank.
Problem 16
Suppose that
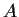
is a commutative algebra with identity over
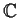
(i.e.,
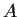
is a commutative ring containing
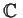
as a subring with
identity). Suppose further that
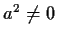
for all nonzero
elements
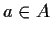
. Show that if the dimension of
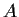
as a vector space
over
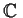
is finite and at least two, then the equations
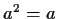
is
satisfied by at least three distinct elements

.
Problem 17
Let
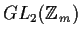
denote the multiplicative group of invertible
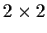
matrices over the ring of integers modulo
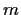
. Find the order of
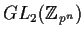
for each prime
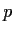
and positive integer
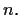



Previous: Fall96
Next: Fall97
Paulo Ney de Souza & Jorge-Nuno Silva
2000-08-10